Em sua vez de jogar, um jogador precisa dar uma tacada na bola branca, de forma a acertar a bola 9 e fazê-la cair em uma das caçapas de uma mesa de bilhar. Como a bola 8 encontra-se entre a bola branca e a bola 9, esse jogador adota a estratégia de dar uma tacada na bola branca em direção a uma das laterais da mesa, de forma que, ao rebater, ela saia em uma trajetória retilínea, formando um ângulo de 90° com a trajetória da tacada, conforme ilustrado na figura.
Com essa estratégia, o jogador conseguiu encaçapar a bola 9. Considere um sistema cartesiano de eixos sobre o plano da mesa, no qual o ponto de contato da bola com a mesa define sua posição nesse sistema. As coordenadas do ponto que representa a bola 9 são (3 ; 3), o centro da caçapa de destino tem coordenadas (6 ; 0) e a abscissa da bola branca é 0,5, como representados na figura.
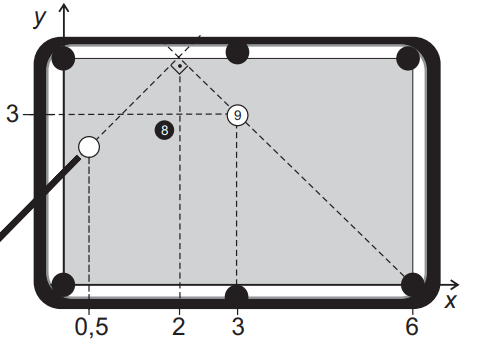
Se a estratégia deu certo, a ordenada da posição original da bola branca era
A) 1,3.
B) 1,5.
C) 2,1.
D) 2,2.
E) 2,5.
Solução
Sabemos que por ser uma reflexão o triângulo formado pelo angulo de noventa e a reta que passa pela bola 9 paralela ao lado é um triângulo isósceles
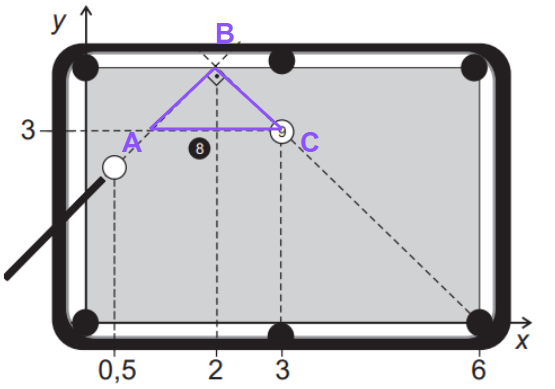
Se o lado AB = BC, A está a mesma distância que C está da bola 8, se a distância é
3 – 2 = 1
A está na coordenada
2 – 1 = 1
Ou seja o ponto A tem par ordenado (1;3)
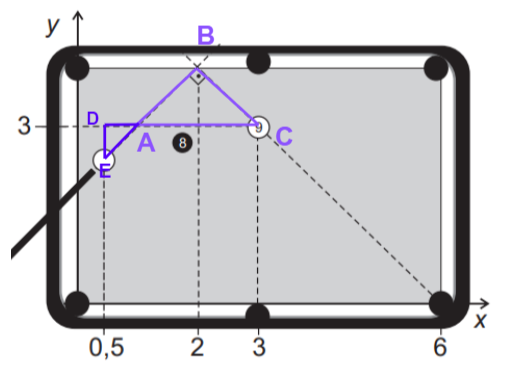
Podemos observar que consequentemente EA será 0,5.
Pela propriedade OPV podemos dizer que o ângulo BAC = EAD, e BAC = 45o já que ABC é isósceles.
Podemos observar que EDA vale 90o, e se BAC vale 45o então DEA também vale 45o, ou seja EDA é isósceles e ED = AD, ou seja
ED = 0,5
consequentemente a ordenada de D é
3 – 0,5 = 2,5
Alternativa E






