Questão 154 – Probabilidade
Um designer de jogos planeja um jogo que faz uso de um tabuleiro de dimensão n x n, com n ≥ 2 no qual cada jogador, na sua vez, coloca uma peça sobre uma das casas vazias do tabuleiro. Quando uma peça é posicionada, a região formada pelas casas que estão na mesma linha ou coluna dessa peça é chamada de zona de combate dessa peça. Na figura está ilustrada a zona de combate de uma peça colocada em uma das casas de um tabuleiro de dimensão 8 x 8.
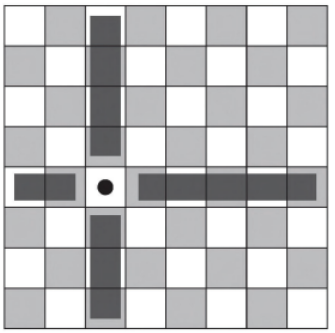
O tabuleiro deve ser dimensionado de forma que a probabilidade de se posicionar a segunda peça aleatoriamente, seguindo a regra do jogo, e esta ficar sobre a zona de combate da primeira, seja inferior a 1/5.
A dimensão mínima que o designer deve adotar para esse tabuleiro é
A) 4 x 4.
B) 6 x 6.
C) 9 x 9.
D) 10 x 10.
E) 11 x 11.
Solução
Em um tabuleiro 8×8 são 14 casas de zona de combate, num total de 64 casas, sendo uma delas ocupada pela peça do adversário, a probabilidade será
14/63 = 2/9
14 porque são duas linhas de 8 que se cruzam, resultando em 15 casas, mas uma delas está ocupada pela peça do adversário, então, pensando dessa forma vamos analisar cada tabuleiro
4 x 4: 6 casas de zona de combate de um total de 16-1 = 15 casas
Probabilidade
6/15 = 2/5 maior que 1/5
6 x 6: 10 casas de zona de combate de um total de 36-1 = 35 casas
Probabilidade
10/35 = 2/7 maior que 1/5
9 x 9: 16 casas de zona de combate de um total de 81-1 = 80 casas
Probabilidade
16/80 = 1/5 igual a 1/5
10 x 10: 18 casas de zona de combate de um total de 100-1 = 99 casas
Probabilidade
18/99 = 2/11 menor que 1/5
11 x 11: 20 casas de zona de combate de um total de 121-1 = 120 casas
Probabilidade
20/120 = 1/6 menor que 1/5
A menor dimensão possível em que a probabilidade é menor que 1/5 é a 10 x 10
Alternativa D
Veja a resolução com mais detalhes no vídeo abaixo!






