Questão 154 – ENEM PPL 2015

Considere que os quarteirões de um bairro tenham sido desenhados no sistema cartesiano, sendo a origem o cruzamento das duas ruas mais movimentadas desse bairro. Nesse desenho, as ruas têm suas larguras desconsideradas e todos os quarteirões são quadrados de mesma área e a medida de seu lado é a unidade do sistema. 

A seguir há uma representação dessa situação, em que os pontos A, B, C e D representam estabelecimentos comerciais desse bairro.

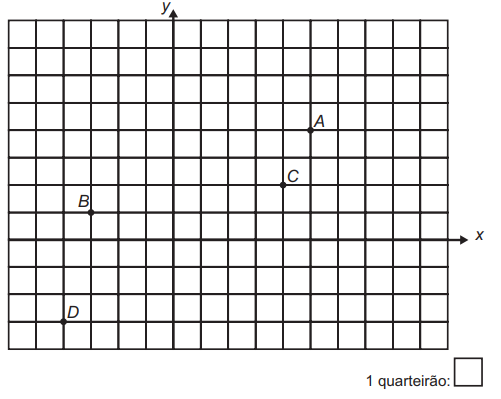
Suponha que uma rádio comunitária, de fraco sinal, garante área de cobertura para todo estabelecimento que se encontre num ponto cujas coordenadas satisfaçam à inequação: x² + y² – 2x – 4y – 31 ≤ 0. 

A fim de avaliar a qualidade do sinal, e proporcionar uma futura melhora, a assistência técnica da rádio realizou uma inspeção para saber quais estabelecimentos estavam dentro da área de cobertura, pois estes conseguem ouvir a rádio enquanto os outros não. 

Os estabelecimentos que conseguem ouvir a rádio são apenas 

A) A e C. 

B) B e C. 

C) B e D. 

D) A, B e C. 

E) B, C e D.

Solução

Sabemos que uma equação de circunferência é dada por

(x-x_c)² + (y-y_c)² = r²

onde x_c e y_c são as coordenadas de centro e r o raio.

E podemos observar que a inequação pode ser escrita dessa forma se separarmos 

Quando no lugar que do igual colocamos ≤, estamos incluindo todos os pontos dentro da circunferência.

então organizando de forma que juntamos os temos

[x² – 2x] + [y² – 4y] – 31 = 0

podemos lembrar que

(x – x_c)² = x²  -2x.x_c + x_c²

e

(y – y_c)² = y²  -2y.y_c + y_c²

Observando a primeira parte temos

x² – 2x, para que 

-2x = -2x.x_c

temos que

x_c = 1

consequentemente a primeira parte deveria ser escrita como

x² – 2x + 1

Enquanto a segunda

y² – 4y

tendo 

-4y = -2y.y_c 

y_c = 2

Consequentemente a segunda parte deveria ser escrita como

y² – 4y + 4

Então teríamos que tirar esses valores +1 e +4 do fator -31 

Tirando +1 de -31 temos

-31 – (+1) = -32

E tirando + 4 de -32 temos

-32 – (+4) = -36

Vamos reescrever a equação da forma ideal

[x² – 2x + 1] + [y² – 4y + 4] – 36 = 0

Escrevendo no formato de circunferência

(x – 1)² + (y – 2)² – 36 = 0

(x – 1)² + (y – 2)² = 36

Tirando a raiz de 36 descobrimos que o raio é 6

(x – 1)² + (y – 2)² = 6²

A circunferência de centro (1,2) e raio 6 será dada a seguir

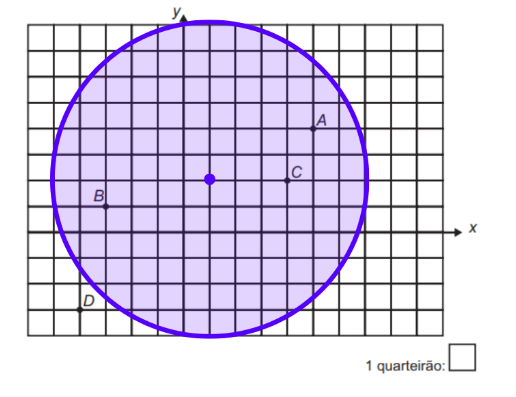
Os pontos incluídos nessa área são os A, B e C.

Alternativa D