Questão 154 – Geometria Espacial
Projetado pelo arquiteto Oscar Niemeyer, o Museu de Arte Contemporânea (MAC) tornou-se um dos cartões-postais da cidade de Niterói (Figura 1)

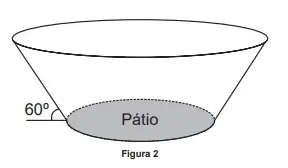
Considere que a forma da cúpula do MAC seja a de um tronco de cone circular reto (Figura 2), cujo diâmetro da base maior mede 50 m e 12 m é a distância entre as duas bases. A administração do museu deseja fazer uma reforma revitalizando o piso de seu pátio e, para isso, precisa estimar a sua área. (Utilize 1,7 como valor aproximado para √3 e 3 para π).
A medida da área do pátio do museu a ser revitalizada, em metro quadrado, está no intervalo
A) [100, 200]
B) [300, 400]
C) [600, 700]
D) [900, 1 000]
E) [1 000, 1 100]
Resolução
Sabemos que o diâmetro da base maior é 50 m e a altura é 12m podemos observar que 50 – 2x = diâmetro do pátio a partir da imagem abaixo

E x pode ser calculado por tg60, sabemos que
Tg60 = 12/x (cateto oposto sobre adjacente)
E também que
Tg60 = √3
Igualando temos
√3 = 12/x
√3x = 12
x = 12/√3
x = 12/1,7 = 7,05
Então o diâmetro será
50 – 2.7,05 = 35,9
A área é dada por
π.r²
Sendo r metade do diâmetro
r = 35,9/2 = 17,95
π.r² = 3*17,95*17,95 = 966,607
Alternativa D
Assista a resolução com mais detalhes no vídeo abaixo!






