Questão 155 – Trigonometria
Para determinar a distância de um barco até a praia, um navegante utilizou o seguinte procedimento: a partir de um ponto A, mediu o ângulo visual α fazendo mira em um ponto fixo P da praia. Mantendo o barco no mesmo sentido, ele seguiu até um ponto B de modo que fosse possível ver o mesmo possível ver o mesmo ponto P da praia, no entanto sob um ângulo visual 2α. A figura ilustra essa situação:
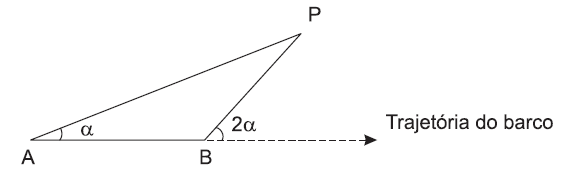
Suponha que o navegante tenha medido o ângulo α = 30° e, ao chegar ao ponto B, verificou que o barco havia percorrido a distância AB = 2 000 m.
Com base nesses dados e mantendo a mesma trajetória, a menor distância do barco até o ponto fixo P será
A) 1 000 m.
B) 1 000 √3 m.
C) 2 000 √3/3 m.
D) 2 000 m
E) 2 000 √3 m.
Solução
Se alfa é 30, 2 vezes alfa é 60 e a menor distância entre o ponto P e a semirreta AB é um segmento de reta que passa pelo ponto P formando um ângulo de 90 graus com AB, chamaremos o ponto de interseção de C.
Sendo PC = x e BC = y, podemos usar a tangente de 30 de tal forma:
Tg 30 = x/(2000 + y)
Sabemos que tg30 = √3/3, então
√3/3 = x/(2000 + y)
2000√3 + √3.y = 3x
Tambem podemos usar a tangente de 60 de tal forma:
Tg 60 = x/y
Sabemos que tg60 = √3, então
√3 = x/y
√3.y = x
Substituindo na primeira equação encontrada
2000√3 + √3.y = 3x
2000√3 + x = 3x
2000√3 = 2x
x = 1000√3
Alternativa B






