Questão 156 – Trigonometria
Uma desenhista projetista deverá desenhar uma tampa de panela em forma circular. Para realizar esse desenho, ela dispõe, no momento, de apenas um compasso, cujo comprimento das hastes é de 10 cm, um transferidor e uma folha de papel com um plano cartesiano. Para esboçar o desenho dessa tampa, ela afastou as hastes do compasso de forma que o ângulo formado por elas fosse de 120o. A ponta seca está representada pelo ponto C, a ponta do grafite está representada pelo ponto B e a cabeça do compasso está representada pelo ponto A conforme a figura.
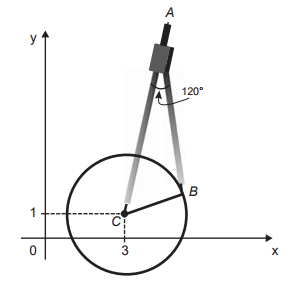
Após concluir o desenho, ela o encaminha para o setor de produção. Ao receber o desenho com a indicação do raio da tampa, verificará em qual intervalo este se encontra e decidirá o tipo de material a ser utilizado na sua fabricação, de acordo com os dados.
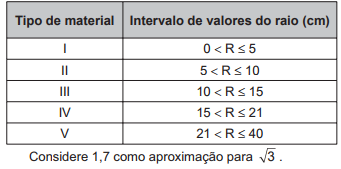
O tipo de material a ser utilizado pelo setor de produção será
A) I
B) II
C) III
D) IV
E) V
Solução
O raio R pode ser calculado pensando: as hastes do compasso tem 10 cm então temos o seguinte triângulo triângulo isósceles
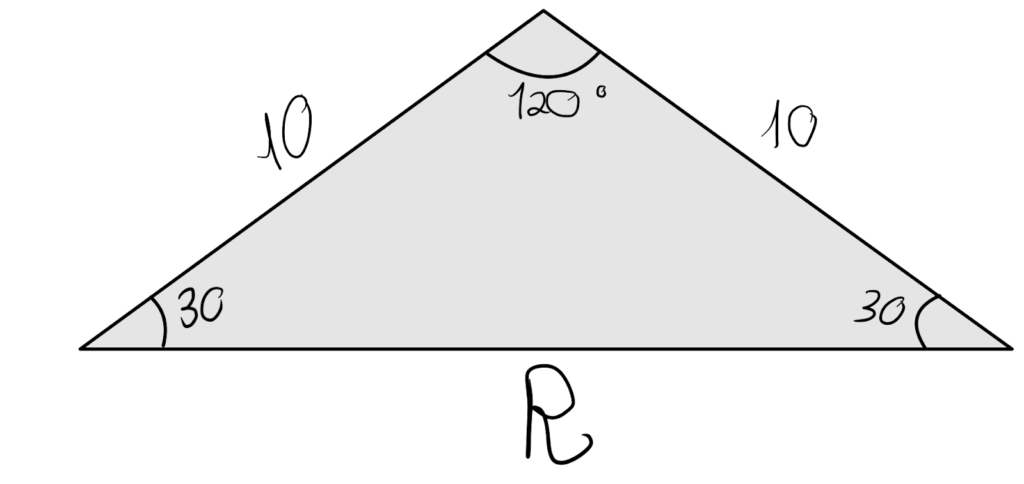
Para calcular R, precisamos usar a altura e formar um triângulo retângulo
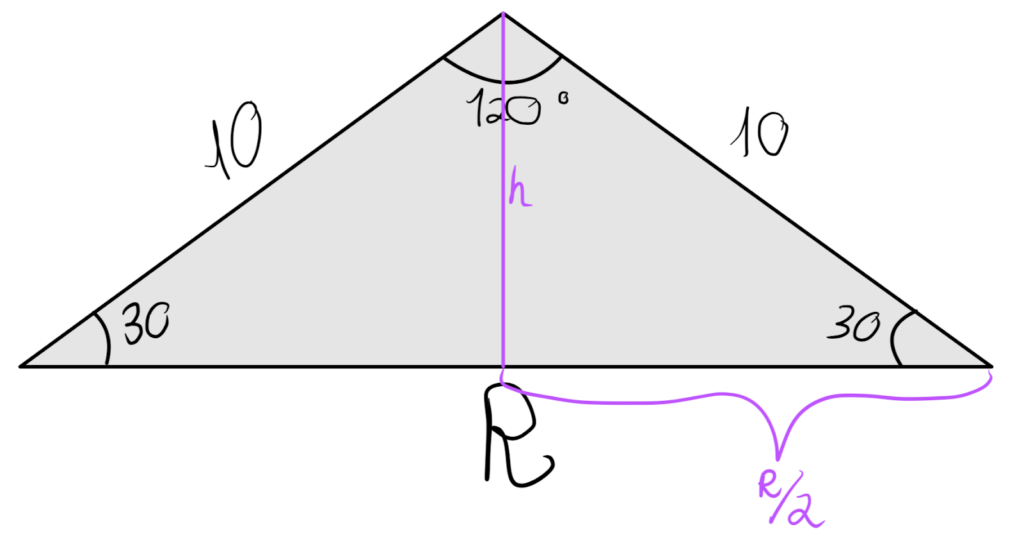
Por cos (30) temos que
Cos(30) = (R/2)/10
E pela tabela temos que
Cos(30) = √3/2
Então
(R/2)/10 = √3/2
Temos então que
R = 10√3 = 10.1,7
R = 17
Alternativa D
Veja a resolução com mais detalhes no vídeo abaixo!






