Questão 156 – Trigonometria
Uma mola é solta da posição distendida conforme a figura. A figura à direita representa o gráfico da posição P (em cm) da massa m em função do tempo t (em segundo) em um sistema de coordenadas cartesianas. Esse movimento periódico é descrito por uma expressão do tipo P(t) = +- A cos(wt) ou P(t) = +- A sen(wt), em que A>0 é a amplitude de deslocamento máximo e w é a frequência, que se relaciona com o período T pela fórmula w = 2π/T .
Considere a ausência de quaisquer forças dissipativas.
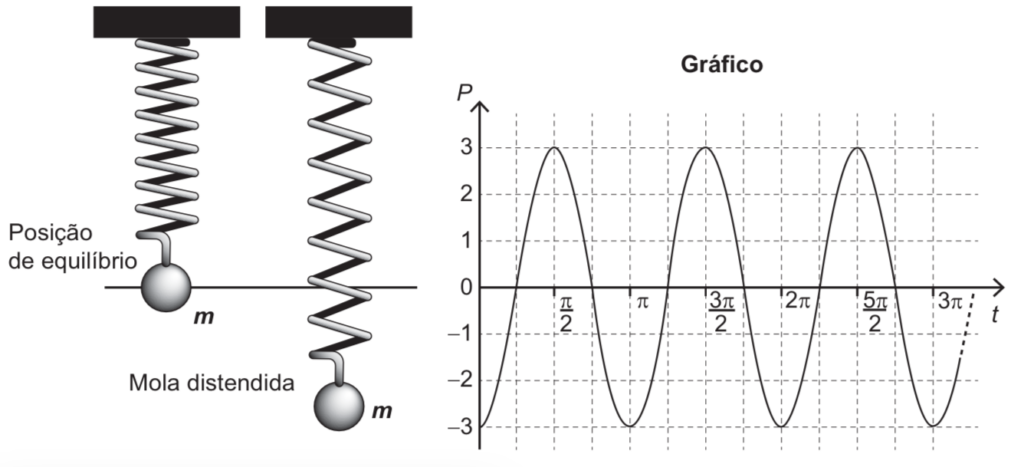
A expressão algébrica que representa as posições P(t) da massa m, ao longo do tempo, no gráfico, é
A) – 3 cos (2t)
B) – 3 sen (2t)
C) 3 cos (2t)
D) – 6 cos (2t)
E) 6 cos (2t)
Solução
Vamos conferir cada alternativa para ver se corresponde com o gráfico, para isso precisamos escolher um par ordenado e substituir nas alternativas.
Vamos usar o par ordenado (π/2 , 3)
Alternativa A) -3.cos (2 . π/2) = -3.cos (π)
-3.cos (π) = (-3) . (-1) = 3
O par ordenado corresponde com o resultado encontrado.
Alternativa B) -3 sen (2t) = -3.sen (2 . π/2) = -3.sen (π)
-3.sen (π) = (-3) . 1 = -3
O par ordenado não corresponde com o resultado encontrado.
Alternativa C) 3.cos (2 . π/2) = 3.cos (π)
3.cos (π) = 3 . (-1) = -3
O par ordenado não corresponde com o resultado encontrado.
Alternativa D) -6.cos (2 . π/2) = -6.cos (π)
-6.cos (π) = (-6) . (-1) = 6
O par ordenado não corresponde com o resultado encontrado.
Alternativa E) 6.cos (2 . π/2) = 6.cos (π)
6.cos (π) = 6 . (-1) = -6
O par ordenado não corresponde com o resultado encontrado.
O único resultado compatível com o par ordenado escolhido é o da
Alternativa A
Veja a resolução com mais detalhes no vídeo abaixo!






