Uma casa lotérica oferece cinco opções de jogos. Em cada opção, o apostador escolhe um grupo de K números distintos em um cartão que contém um total de N números disponíveis, gerando, dessa forma, um total de C combinações possíveis para se fazer a marcação do cartão. Ganha o prêmio o cartão que apresentar os K números sorteados. Os valores desses jogos variam de R$ 1,00 a R$ 2,00, conforme descrito no quadro.
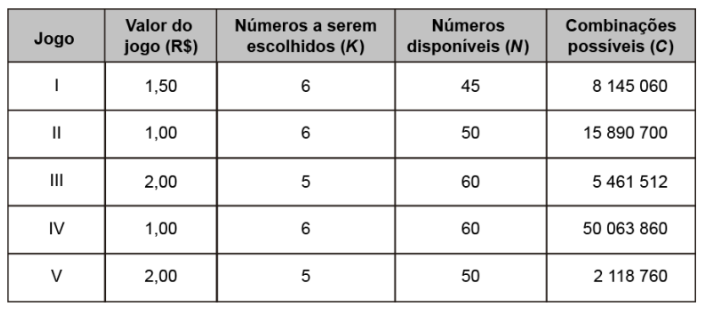
Um apostador dispõe de R$ 2,00 para gastar em uma das cinco opções de jogos disponíveis.
Segundo o valor disponível para ser gasto, o jogo que oferece ao apostador maior probabilidade de ganhar prêmio é o
A) I.
B) II.
C) III.
D) IV.
E) V.
Resolução
A probabilidade é dada pela seguinte razão
P = quantidade de jogadas em que ganha/total de combinações possíveis.
Vamos avaliar cada opção, considerando que se o apostador jogar 1 vez ele pode ganhar 1 jogada e ele tem disponível 2 reais
I: Pode jogar 1 jogo que custa 1,50, probabilidade de ganhar é 1/8 145 060
II: Pode jogar 2 jogos que custam 1,00, probabilidade de ganhar é 2/15 890 700
III: Pode jogar 1 jogo que custa 2,00, probabilidade de ganhar é 1/5 461 512
IV: Pode jogar 2 jogos que custam 1,00, probabilidade de ganhar é 2/50 063 860
V: Pode jogar 1 jogo que custa 2,00, probabilidade de ganhar é 1/2 118 760
Para comparar qual fração é maior precisamos lembrar que se o numerador é igual, a maior fração é a que tem MENOR denominador.
Vamos então comparar todas as frações com numerador 1
1/8.145.060 < 1/5.461.512 < 1/2.118.760
Então desses 3 o maior é 1/2.118.760
Comparando os com numerador 2
2/50 063 860 < 2/15 890 700
Desses 2 o maior é 2/15.890.700
Agora para comparar os de numeradores diferentes vamos simplificar o de numerador 2
2/15.890.700 = 1/7.945.350
Comparando os dois vemos que
1/7.945.350 < 1/2.118.760
Então a maior probabilidade é do jogo V
Alternativa E






