A distância atual entre os centros da Terra e de seu satélite natural (Lua) é de 384 405 km. Essa distância aumenta 4 cm por ano. O centro de gravidade do sistema (ou baricentro), formado pelos dois corpos celestes, está a 1 737 km da superfície da Terra, e essa distância diminui gradativamente. Este centro de gravidade se localizará fora da Terra em 3 bilhões de anos e, com isso, a Lua deixará de ser nosso satélite, tornando-se um planeta.
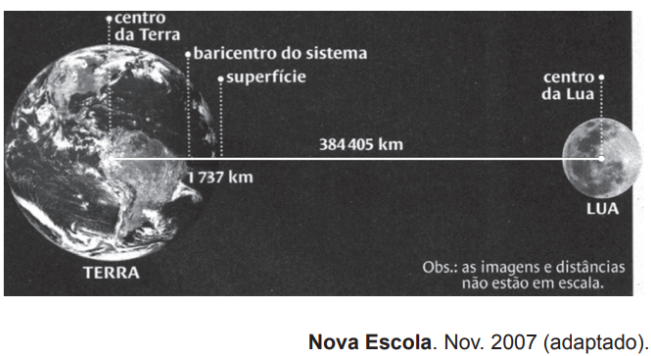
Quantos centímetros por ano, em média, o centro de gravidade do sistema se aproximará da superfície terrestre, até que a Lua se torne um planeta?
A) 0,0579
B) 0,5790
C) 5,7900
D) 12,8135
E) 17,2711
Solução
A questão diz que o baricentro formado pelos 2 corpos celestes estar a 1737 km convertendo temos, 173700000 cm ou 1 737*105
Agora é só fazer a divisão pelo tempo que é 3 bilhões de anos ou 3*10^9
1 737*105 /3*109 =
1 737 / 3*104 = 0,0579 cm por ano.
Alternativa A






