Vítor deseja revestir uma sala retangular de dimensões 3 m x 4 m, usando um tipo de peça de cerâmica. Em uma pesquisa inicial, ele selecionou cinco tipos de peças disponíveis, nos seguintes formatos e dimensões:
• Tipo I: quadrados, com 0,5 m de lado.
• Tipo II: triângulos equiláteros, com 0,5 m de lado.
• Tipo III: retângulos, com dimensões 0,5 m x 0,6 m.
• Tipo IV: triângulos retângulos isósceles, cujos catetos medem 0,5 m.
• Tipo V: quadrados, com 0,6 m de lado.
Analisando a pesquisa, o mestre de obras recomendou que Vítor escolhesse um tipo de piso que possibilitasse a utilização do menor número de peças e não acarretasse sobreposições ou cortes nas cerâmicas.
Qual o tipo de piso o mestre de obras recomendou que fosse comprado?
A) Tipo I.
B) Tipo II.
C) Tipo III.
D) Tipo IV.
E) Tipo V.
Solução
Tipo I: seria necessário 3/0,5 = 6 peças no comprimento e 4/0,5 = 8 peças na largura, ou seja, 6 . 8 = 48 peças no total.
Tipo II: como são triângulos equiláteros, não seria possível revestir a sala retangular, uma vez que, ainda que uníssemos dois triângulos equiláteros, não seria possível formar um ângulo de 90 graus. Observe a imagem:
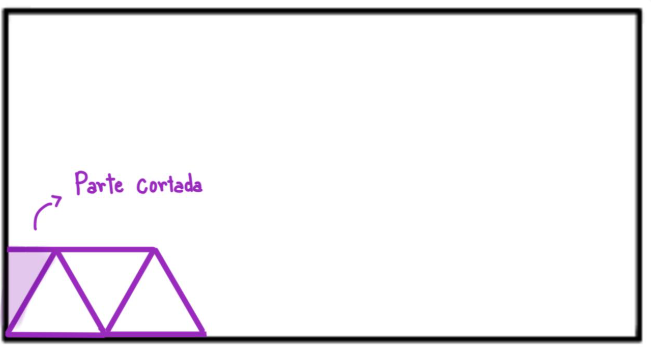
Tipo III: seria necessário 4/0,5 = 8 peças no comprimento e 3/0,6 = 5 peças na largura, ou seja, 8 . 5 = 40 peças no total.
Tipo IV: como são triângulos isósceles de lado 0,5, a união de dois formaria um quadrado. Portanto, teríamos um quadrado de 0,5 a cada duas peças de triângulo. Isso significa dizer que precisaríamos de 3/0,5 . 2 = 12 peças no comprimento e 4/0,5 . 2 = 16 peças na largura. Observe que é o dobro da quantidade usada pelo tipo I, o que nos faz descartar essa alternativa antes de concluir o cálculo.
Tipo V: como 4 não pode ser dividido por 0,6 para formar um número inteiro, e o comando exige que não haja cortes, então podemos desconsiderar essa alternativa.
Portanto, o menor custo seria com o tipo III, com 40 peças.
Alternativa C






