Questão 157 – Geometria Espacial
Num parque aquático existe uma piscina infantil na forma de um cilindro circular reto, de 1 m de profundidade e volume igual a 12 m³, cuja base tem raio R e centro O. Deseja-se construir uma ilha de lazer seca no interior dessa piscina, também na forma de um cilindro circular reto, cuja base estará no fundo da piscina e com centro da base coincidindo com o centro do fundo da piscina, conforme a figura. O raio da ilha de lazer será r. Deseja-se que após a construção dessa ilha, o espaço destinado à água na piscina tenha um volume de, no mínimo, 4 m³.
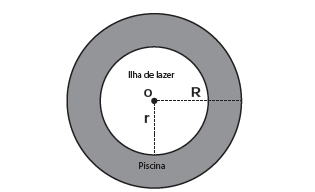
Considere 3 como valor aproximado para π
Para satisfazer as condições dadas, o raio máximo da ilha de lazer r, em metros, estará mais próximo de
A) 1,6
B) 1,7
C) 2,0
D) 3,0
E) 3,8
Solução
Precisamos que o volume da piscina (Vp) menos o da ilha de lazer (Vi) seja maior ou igual a 4
Sabemos que o volume da piscina é dado por 12 m3 e o volume da ilha de lazer é π.r2.1, ou seja queremos que
12 – π.r2.1 > 4
12 – 3r2 > 4
-3r2 > 4 – 12
-3r2 > -8
Multiplicando os dois lados por (-1) temos
3r2 < 8
r2 < 8/3
r < √(8/3)
r < 1,64
A alternativa com o maior valor que se encaixa no intervalo proposto é 1,6
Alternativa A






