Questão 157 – Enem PPL 2013

Uma fábrica utiliza sua frota particular de caminhões para distribuir as 90 toneladas de sua produção semanal. Todos os caminhões são do mesmo modelo e, para aumentar a vida útil da frota, adota-se a política de reduzir a capacidade máxima de carga de cada caminhão em meia tonelada. Com essa medida de redução, o número de caminhões necessários para transportar a produção semanal aumenta em 6 unidades em relação ao número de caminhões necessários para transportar a produção, usando a capacidade máxima de carga de cada caminhão. 

Qual é o número atual de caminhões que essa fábrica usa para transportar a produção semanal, respeitando-se a política de redução de carga? 

A) 36 

B) 30 

C) 19 

D) 16 

E) 10 

Resolução

Vamos chamar de C a capacidade máxima de carga (em toneladas) de cada caminhão antes da redução.

Com a política de redução de carga, a nova capacidade de cada caminhão será C−0,5 toneladas.

Sem a redução de carga, o número de caminhões necessários para transportar 90 toneladas é:

90/C

Com a redução de 0,5 tonelada na capacidade de cada caminhão, o número de caminhões necessários será:

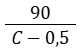
Sabemos que o número de caminhões com a capacidade reduzida aumenta em 6 unidades em relação ao número de caminhões com a capacidade máxima. Então, temos:

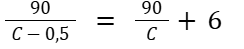
 Multiplicamos ambos os lados por C(C−0,5) para eliminar os denominadores:

90C = 90(C – 0,5) + 6C(C – 0,5)

90C = 90C – 45 + 6C² – 3C

6C² – 3C – 45 = 0

Dividindo tudo por 3

2C² – C – 15 = 0

Calculando a raiz da equação temos

Delta = 1 – 4.2.(-15) = 121

C = (1 士  √121)/4 = (1 士 11)/4

C₁ = -10/4 = -2,5

C₂ = 12/4 = 3

A raiz válida para essa ocasião é a positiva, já que estamos falando de números de caminhões e toneladas.

Se o número de caminhões será C = 3, o de toneladas será

90/3 = 30

Com mais 6 caminhões adicionados, teremos 36.

Alternativa A