Questão 157 – Geometria Espacial
Uma cidade enfrenta racionamento no abastecimento de água. Para minimizar os efeitos da falta de água para seus hóspedes, o gerente de um hotel pretende substituir a caixa-d’água existente por um reservatório. Sabe-se que o consumo médio diário do hotel é de 10 mil litros de água. Mantido o consumo médio diário, o gerente quer que o novo reservatório, uma vez cheio, seja capaz de suprir as necessidades do hotel por, pelo menos, 6 dias completos, mesmo que não haja abastecimento de água nesse período.
O espaço de que o hotel dispõe para instalar o novo reservatório tem formato retangular com largura de 5 m e comprimento de 6 m. O gerente analisa cinco opções disponíveis para esse reservatório.
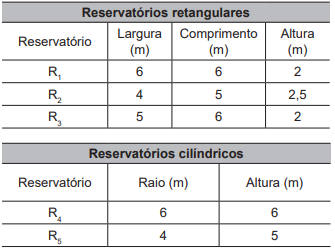
A opção de reservatório que atende à necessidade do hotel e que cabe no espaço disponível é
A) R1 .
B) R2 .
C) R3 .
D) R4 .
E) R5.
Resolução
Se gasta 10 mil litros de água por dia, em 6 dias são gastos 60 mil litros de água.
Queremos um reservatório com essa capacidade que caiba no espaço reservado!
R1 não cabe pois tem largura maior do que o espaço.
R4 e R5 tem diâmetros maiores que a menor dimensão do espaço.
Agora vamos calcular os volumes de:
R2 : 4 . 5 . 2,5 = 50 m³ que corresponde a 50 000 L, não sendo suficiente para abastecer por 6 dias.
R3 : 5 . 6. 2 = 60 m³, correspondendo a 60 000 L, exatamente a capacidade necessária.
Alternativa C
Assista a resolução com mais detalhes no vídeo abaixo!






