Questão 158 – Análise Combinatória
Três amigos, André, Bernardo e Carlos, moram em um condomínio fechado de uma cidade. O quadriculado representa a localização das ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho nesse condomínio, em que nos pontos A, B e C estão localizadas as casas de André, Bernardo e Carlos, respectivamente.
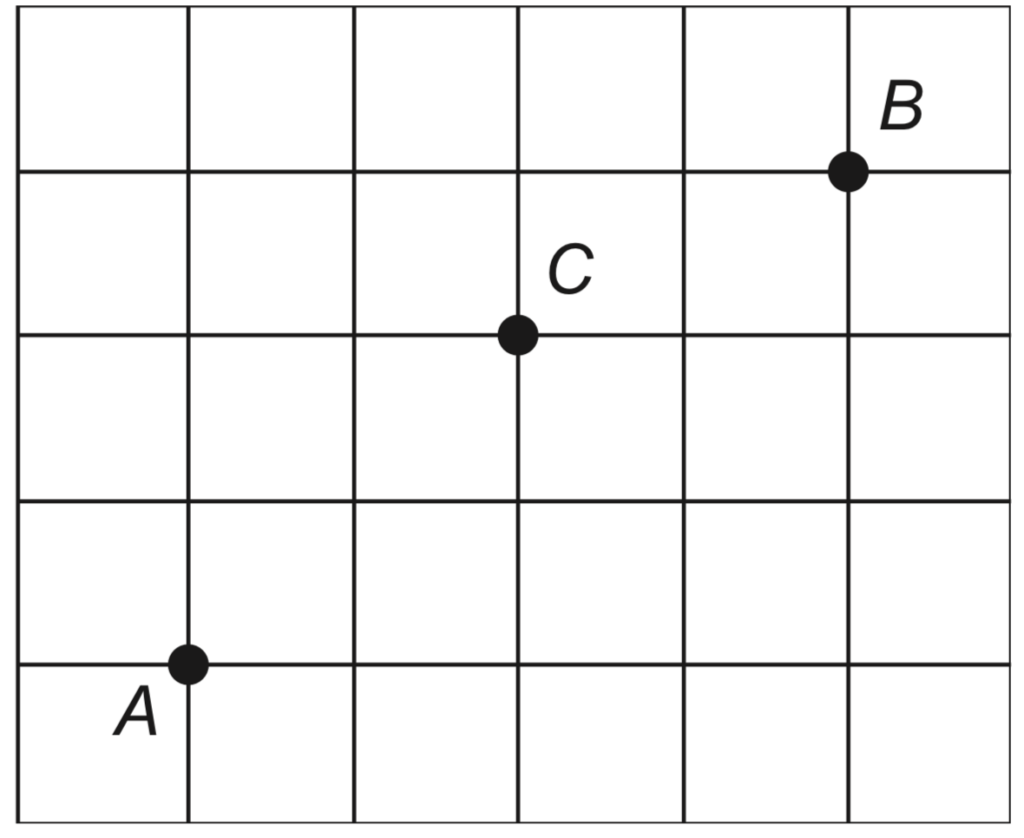
André deseja deslocar-se da sua casa até a casa de Bernardo, sem passar pela casa de Carlos, seguindo ao longo das ruas do condomínio, fazendo sempre deslocamentos para a direita (→) ou para cima (↑), segundo o esquema da figura.
O número de diferentes caminhos que André poderá utilizar para realizar o deslocamento nas condições propostas é
A) 4
B) 14
C) 17
D) 35
E) 48
Solução
Indo de A a B é necessário deslocar 3 vezes para cima e 4 para a direita, independente da ordem, sempre fazendo esses movimentos Carlos chegará a B.
Vamos usar a fórmula de permutação com repetição.
7!/(4!.3!) = 35
Para que nesse trajeto ele passe de A para C ele precisa andar 2 vezes para cima e 2 vezes para diretos e de C para B é necessário movimentar 2 vezes para direita e 1 vez para cima. Multiplicando essas permutações temos:
4!/(2!.2!) . 3!/2! = 18
Como não queremos que ele passe por C o total de possibilidades é 35 – 18 = 17
Alternativa C
Veja a resolução com mais detalhes no vídeo abaixo!







Aí sim mulekão!!