Questão 158 – Função de 2o grau
Um projétil é lançado por um canhão e atinge o solo a uma distância de 150 metros do ponto de partida. Ele percorre uma trajetória parabólica, e a altura máxima que atinge em relação ao solo é de 25 metros.
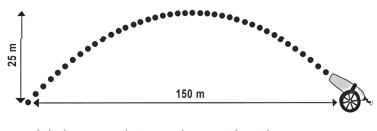
Admita um sistema de coordenadas xy em que no eixo vertical y está representada a altura e no eixo horizontal x está representada a distância, ambas em metro. Considere que o canhão está no ponto (150; 0) e que o projétil atinge o solo no ponto (0; 0) do plano xy. A equação da parábola que representa a trajetória descrita pelo projétil é
A) y = 150x − x2
B) y = 3 750x − 25x2
C) 75y = 300x − 2x2
D) 125y = 450x − 3x2
E) 225y = 150x − x2
Resolução
Sendo a equação no formato y = ax² + bx + c e a parábola corta o eixo na origem, então c = 0.
Então temos a equação
y = ax² + bx
Também sabemos que temos o ponto (150,0) que satisfaz a equação, então, substituindo os valores de x e y na equação, temos
0 = 150²a + 150b
Sabemos que yv = 25, e como o xv é o ponto exatamente no meio das duas raízes, xv = 75. O par ordenado do vértice é (75,25), podemos substituir na equação e formar um sistema de equações
25 = 75²a + 75b
0 = 150²a + 150b
Isolando na segunda equação temos
b = -150²a/150
b = -150a
Substituindo na primeira equação
25 = 75.75a – 75.150a
25 = -75.75a
a = -25/75.75
a = -1/225
Substituindo na equação onde isolamos b
b = 150/225
então a equação é
y = -x²/225 + 150x/225
se multiplicarmos a equação toda por 225, temos
225y = -x² + 150x
Alternativa E






