Questão 159 – Geometria Plana
Um brinquedo chamado pula-pula, quando visto de cima, consiste de uma cama elástica com contorno em formato de um hexágono regular.
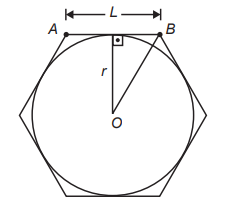
Se a área do círculo inscrito no hexágono é 3π metros quadrados, então a área do hexágono, em metro quadrado, é

Resolução
Se a área do círculo é 3π então o raio r será
3π = πr²
r = √3
Podemos observar que o r forma um triângulo retângulo com metade do lado do hexágono em que a hipotenusa é a distância do centro ao vértice B.
Pelas propriedades do hexágono regular, sabemos que o segmento OB é igual ao segmento AB, então vale L.
Vamos usar pitágoras para calcular L nesse triângulo retângulo
r² + (L/2)² = L²
substituindo r
√3² + L²/4 =L²
3 = L² – L²/4
3 = 3L²/4
L² = 4
L = 2
A área do hexágono regular é dada por
3√3L²/2 = 3√3.4/2 = 6√3 m²
Alternativa B






