Questão 160 – ENEM 2012

Questão 160 – Geometria Plana

Para decorar a fachada de um edifício, um arquiteto projetou a colocação de vitrais compostos de quadrados de lado medindo 1 m, conforme a figura a seguir.

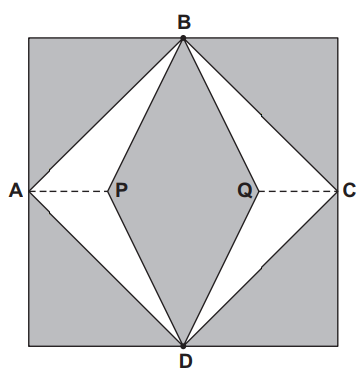
Nesta figura, os pontos A, B, C e D são pontos médios dos lados do quadrado e os segmentos AP e QC medem 1/4 da medida do lado do quadrado. Para confeccionar um vitral, são usados dois tipos de materiais: um para a parte sombreada da figura, que custa R$ 30,00 o m², e outro para a parte mais clara (regiões ABPDA e BCDQB), que custa R$ 50,00 o m².

De acordo com esses dados, qual é o custo dos materiais usados na fabricação de um vitral? 

A) R$ 22,50

B) R$ 35,00

C) R$ 40,00

D) R$ 42,50

E) R$ 45,00

Solução

Vamos calcular a área clara.

O lado do quadrado ABCD é dado por pitágoras.

Sabemos que a medida do vértice até o ponto B é igual a metade do lado do quadrado maior que é 1m, igualmente para a medida até o ponto A.

Fazendo pitágoras temos que, seno L o lado AB:

L² = 0,5² + 0,5²

L² = 0,25 + 0,25

L = √0,5

Vamos agora calcular a área desse quadrado

L.L = 0,5 m²

A área clara corresponde a área de ABCD menos a área de BPDQ, agora vamos calcular BPDQ

Podemos separar essa área em dois triângulos de base PQ que mede exatamente 0,5 m, a altura desses triângulos também é dada pela metade do lado do quadrado de 1m, ou seja:

A área do triângulo BPQ é

0,5.0,5/2 = 0,125

Como o triângulo é igual, a soma dos dois é

0,125 + 0,125 = 0,25 m²

Então já podemos calcular a área clara

0,5 – 0,25  = 0,25 m²

Consequentemente a área total sombreada será

1 – 0,25 = 0,75 m²

O preço de 0,25 m² do material claro é

0,25.50 = 12,50 reais

E o preço de 0,75 m² do material sombreado é

0,75.30 = 22,50 reais

Somando esses valores, cada vitral custa

12,50 + 22,5 = 35 reais

Alternativa B