Durante seu treinamento, um atleta percorre metade de uma pista circular de raio R, conforme figura a seguir. A sua largada foi dada na posição representada pela letra L, a chegada está representada pela letra C e a letra A representa o atleta. O segmento LC é um diâmetro da circunferência e o centro da circunferência está representado pela letra F.
Sabemos que, em qualquer posição que o atleta esteja na pista, os segmentos LA e AC são perpendiculares. Seja θ o ângulo que o segmento AF faz com segmento FC.
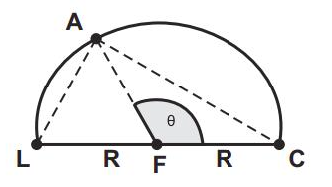
Quantos graus mede o ângulo θ quando o segmento AC medir R durante a corrida?
A) 5 graus
B) 30 graus
C) 60 graus
D) 90 graus
E) 120 graus
Solução
Nessa questão basta notar que o segmento FC vale R e o segmento FA, também vale R, sendo assim, no momento que AC valer R, forma-se um triângulo equilátero AFC, de lados R.
Dessa forma, como a soma dos ângulos internos de um triângulo deve ser 180º e o triângulo equilátero deve ter 3 lados e 3 ângulos iguais, sabemos que o ângulo teta vale 60º, pois 180/3 = 60.
Alternativa C






