Questão 161 – ENEM 2015

Questão 161 – Geometria Plana

Uma indústria produz malhas de proteção solar para serem aplicadas em vidros, de modo a diminuir a passagem de luz, a partir de fitas plásticas entrelaçadas perpendicularmente. Nas direções vertical e horizontal, são aplicadas fitas de 1 milímetro de largura, tal que a distância entre elas é de (d – 1) milímetros, conforme a figura. O material utilizado não permite a passagem da luz, ou seja, somente o raio de luz que atingir as lacunas deixadas pelo entrelaçamento consegue transpor essa proteção.

A taxa de cobertura do vidro é o percentual da área da religião coberta pelas fitas da mala, que são colocadas paralelamente às bordas do vidro.

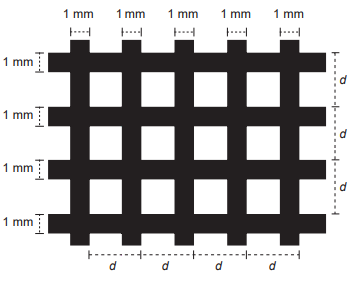
Essa indústria recebeu a encomenda de uma malha de proteção solar para ser aplicada em um vidro retangular de 5 m de largura por 9 m de comprimento.

A medida de d, em milímetros, para que a taxa de cobertura da malha seja de 75% é

A) 2

B) 1

C) 11/3

D) 4/3

E) 2/3

Solução

Queremos que a razão da área coberta sobre a área total seja maior que 75%, para isso precisamos garantir que a área expressada por A abaixo tenha 75% coberta e 25% descobertas já que ela se replica múltiplas vezes ao longo da malha.

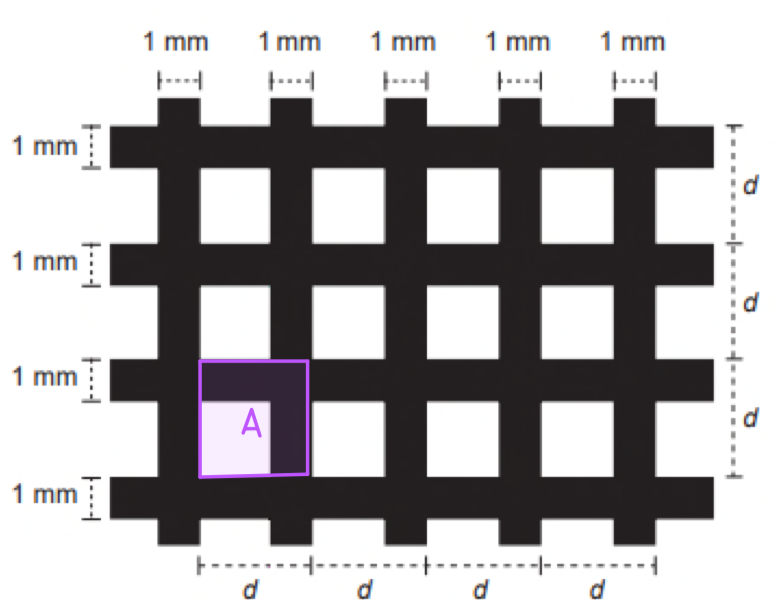
A é um quadrado de lado d, e a área descoberta é um quadrado de lado (d – 1)

Então queremos que

(d – 1)²/d² = 25/100

(d – 1)²/d² = 1/4

Tirando raiz quadrada dos dois lados temos

(d – 1)/d = 1/2

Multiplicando cruzado

2d – 2 = d

2d – d = 2

d = 2

Alternativa A