Questão 162 – Função de 1o Grau
Em uma cidade, o valor total da conta de energia elétrica é obtido pelo produto entre o consumo (em kWh) e o valor da tarifa do kWh (com tributos), adicionado à Cosip (contribuição para custeio da iluminação pública), conforme a expressão:
Valor do kWh (com tributos) x consumo (em kWh) + Cosip
O valor da Cosip é fixo em cada faixa de consumo. O quadro mostra o valor cobrado para algumas faixas.
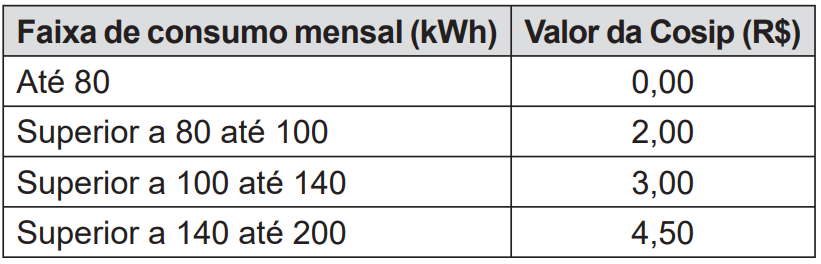
Suponha que, em uma residência, todo mês o consumo seja de 150 kWh, e o valor do kWh (com tributos) seja de R$ 0,50. O morador dessa residência pretende diminuir seu consumo mensal de energia elétrica com o objetivo de reduzir o custo total da conta em pelo menos 10%.
Qual deve ser o consumo máximo, em kWh, dessa residência para produzir a redução pretendida pelo morador?
A) 134,1
B) 135,0
C) 137,1
D) 138,6
E) 143,1
Solução
Se o consumo mensal da família é 150kWh com 0,50 centavos por kWh e uma tarifa de 4,50 reais, o gasto mensal é
150.0,50 + 4,50 = 79,50
Queremos uma redução de 10%, ou seja o novo preço deve ser
79,50 . 0,90 = 71,55 reais
Vamos analisar as faixas de maior consumo.
Superior a 140 até 200: com a cosip a 4,50, restam
71,55 – 4,50 = 67,05 de taxa
Sendo o preco do kWh 0,50 centavos, serão necessários
67,05/0,50 = 134,10 kWh, mas na faixa o valor mínimo é 140, então não se encontra nessa faixa.
Superior a 100 até 140: com a cosip a 3,00 restam
71,55 – 3 = 68,55 reais de taxa
Dividindo pelo preço de cada kWh
68,55/0,5 = 137,10
Que se encontra nessa faixa, ou seja, esse é a maior quantidade de kWh que deve ser consumida.
Alternativa C






