Questão 162 – Geometria Analítica
O fisiologista inglês Archibald Vivian Hill propôs, em seus estudos, que a velocidade V de contração de um músculo ao ser submetido a um peso p é dada pela equação (p + a) (v +b) = K, com a, b e K constantes.
Um fisioterapeuta, com o intuito de maximizar o efeito benéfico dos exercícios que recomendaria a um de seus pacientes, quis estudar essa equação e a classificou desta forma:
O fisioterapeuta analisou a dependência entre v e p na equação de Hill e a classificou de acordo com sua representação geométrica no plano cartesiano, utilizando o par de coordenadas (p. V). Admita que K> 0.
Disponível em: http://rspb.royalsocietypublishing.org. Acesso em: 14jul2015 (adaptado).
O gráfico da equação que o fisioterapeuta utilizou para maximizar o efeito dos exercícios é do tipo
A) Semirreta oblíqua.
B) semirreta horizontal.
C) ramo de parábola.
D) arco de circunferência.
E) ramo de hipérbole.
Solução
Queremos isolar o v para ficar com a aparência de uma função de variável p
(p + a) (v +b) = K
v = K/(p + a) – b
Podemos observar que ao p se aproximar ao valor de -a, v tende ao infinito, e quão maior for p, mais próximo de – b v se encontra, ou seja o formato da função são duas hipérboles
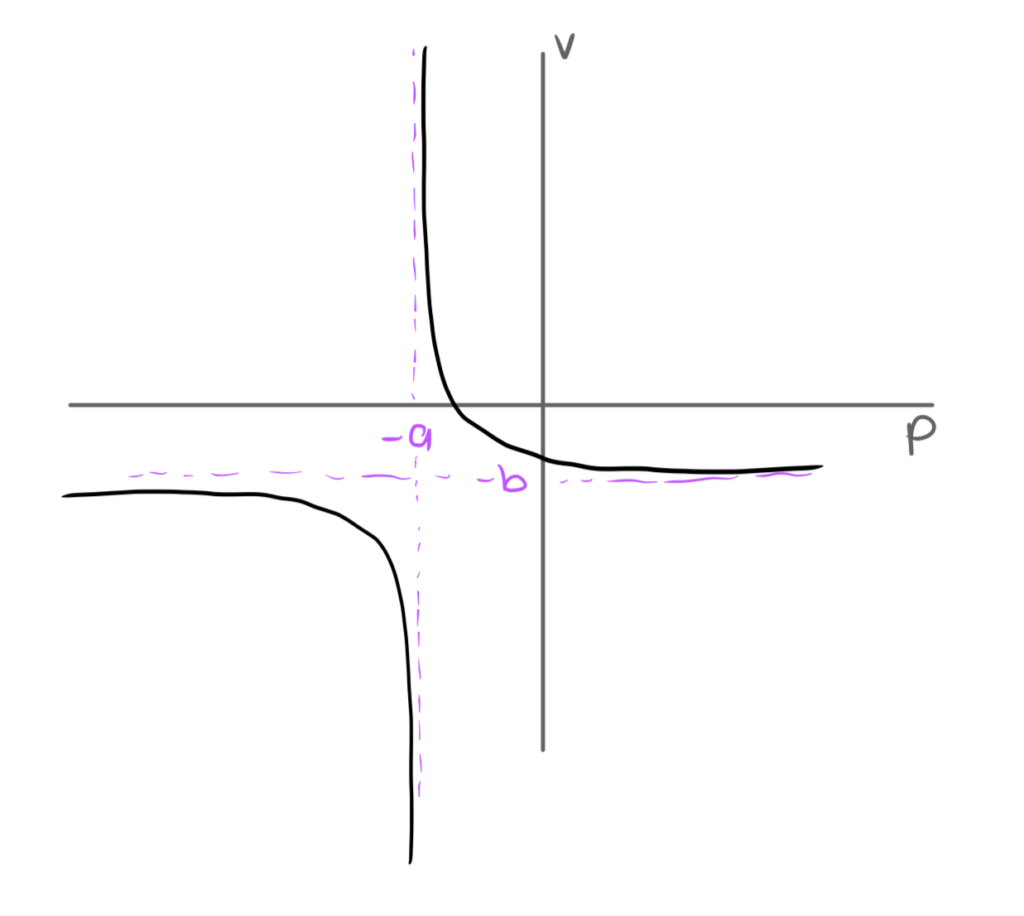
Se v e p são apenas valores positivos podemos dizer que a imagem é um ramo de uma hipérbole.
Alternativa E
Veja a resolução com mais detalhes no vídeo abaixo!






