Um arquiteto deseja construir um jardim circular de 20 m de diâmetro. Nesse jardim, uma parte do terreno será reservada para pedras ornamentais. Essa parte terá a forma de um quadrado inscrito na circunferência, como mostrado na figura. Na parte compreendida entre o contorno da circunferência e a parte externa ao quadrado, será colocada terra vegetal. Nessa parte do jardim, serão usados 15 kg de terra para cada m². A terra vegetal é comercializada em sacos com exatos 15 kg cada. Use 3 como valor aproximado para π.

O número mínimo de sacos de terra vegetal necessários para cobrir a parte descrita do jardim é
A) 100.
B) 140.
C) 200.
D) 800.
E) 1 000.
Solução
Basta subtrair a área da circunferência de diâmetro 20 m ,ou seja R = 10
πR² = π10² = 100π = 100.3 = 300
E subtrair a área do quadrado, para calcular a área do quadrado deve se notar o seguinte triângulo
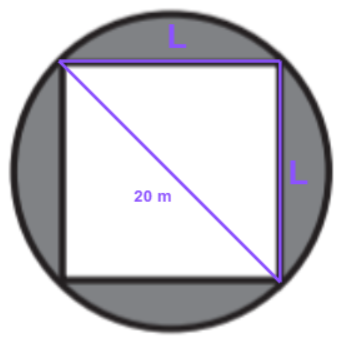
Por pitágoras conseguimos calcular o L
20² = L² + L²
20² = 2L²
L² = 20²/2 = 400/2 = 200
A área do quadrado é L², então a área sombreada será
300 – 200 = 100 m²
Se são 15 kg para cada m² e cada saco vende 15 kg, serão necessários
100.15/15 = 100 sacos
Alternativa A






