Questão 162 – Lógica
Em um jogo de tabuleiro, a pontuação é marcada com fichas coloridas. Cada ficha vermelha vale um ponto. Três fichas vermelhas podem ser trocadas por uma azul, três fichas azuis podem ser trocadas por uma branca, e três fichas brancas podem ser trocadas por uma verde. Ao final do jogo, os jogadores A, B e C terminaram, cada um, com as quantidades de fichas, conforme a tabela seguinte:
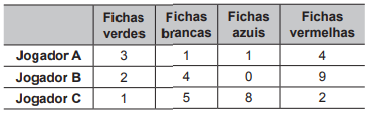
De acordo com essa tabela, as classificações em primeiro, segundo e terceiro lugares ficaram, respectivamente, para os jogadores
A) A, B e C.
B) B, A e C.
C) C, B e A.
D) B, C e A.
E) C, A e B.
Resolução
Se cada vermelha vale 1 ponto e a ficha azul são 3 vermelhas, então a
Azul vale 3 pontos.
Se a cada 3 azuis você pode obter 1 branca, então a
Branca vale 3.3 = 9 pontos.
Se a cada 3 brancas você pode obter 1 verde, então a
Verde vale 3.9 = 27 pontos.
Vamos então contabilizar os pontos de cada jogador
A: 3.27 + 1.9 + 1.3 + 4.1 = 81 + 9 + 3 + 4 = 97 pontos
B: 2.27 + 4.9 + 0.3 + 9.1 = 54 + 36 + 0 + 9 = 99 pontos
C: 1.27 + 5.9 + 8.3 + 2.1 = 27 + 45 + 24 + 2 = 98 pontos
A ordem de classificação foi
B, C e A
Alternativa D






