Questão 164 AMARELA – Geometria Espacial
Um artista plástico esculpe uma escultura a partir de um bloco de madeira de lei, em etapas. Inicialmente, esculpe um cone reto com 36 cm de altura e diâmetro da base medindo 18 cm. Em seguida, remove desse cone um cone menor, cujo diâmetro da base mede 6 cm, obtendo, assim, um tronco de cone, conforme ilustrado na figura
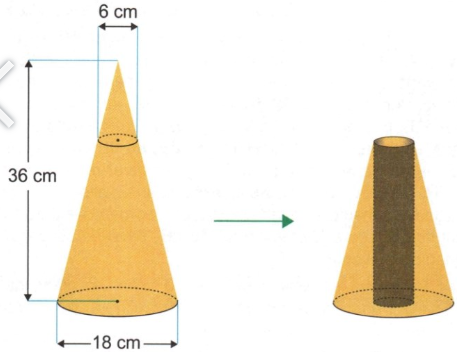
Em seguida, perfura esse tronco de cone, removendo cilindro reto, de diâmetro 6 cm, cujo eixo de simetria é o mesmo do cone original. Dessa forma, ao final, a escultura tem a forma de um tronco de cone com uma perfuração cilíndrica de base a base.
O tipo de madeira utilizada para produzir essa escultura tem massa igual a 0,6 g por centímetro cúbico de volume.
Utilize 3 como aproximação para pi.
Qual é a massa, em grama, dessa escultura?
A) 1998,8
B) 1296,0
C) 1360,8
D) 4665,6
E) 4860,0
Solução
Calculando a altura do tronco por razão de triângulos temos
36/18 = h/6
h = 12
então o volume é dado pelo volume do cone maior de base 18 e altura 36, menos o volume do cone menor de base 6 com altura 12:
Vtronco = 3.9².36/3 – 3.3².12/3
Vtronco = 81.36 – 9.12 = 2916 – 108 = 2808cm³
Vcilindro = 3.3².24 = 648cm³
V = 2808 – 648 = 2160cm³
Temos 0,6g por centímetro cúbico:
0,6 . 2160 = 1296
Alternativa B
Veja a resolução com mais detalhes no vídeo abaixo!






