Questão 164 – Trigonometria
Ao morrer, o pai de João, Pedro e José deixou como herança um terreno retangular de 3 km x 2 km que contém uma área de extração de ouro delimitada por um quarto de círculo de raio 1 km a partir do canto inferior esquerdo da propriedade. Dado o maior valor da área de extração de ouro, os irmãos acordaram em repartir a propriedade de modo que cada um ficasse com a terça parte da área de extração, conforme mostra a figura.
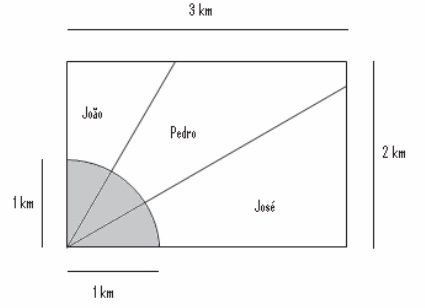
Em relação à partilha proposta, constata-se que a porcentagem da área do terreno que coube a João corresponde, aproximadamente, a
(considere √3/3 = 0,58)
A) 50%.
B) 43%
C) 37%
D) 33%
E) 19%
Solução
Conseguimos calcular a área do triângulo correspondentes à área de João.
Sabemos que 1/4 de um círculo tem 90o, então se esse ângulo foi dividido em 3 partes, cada ângulo tem 30o.
Vamos calcular a área de João:
Como é um triângulo retângulo, a área é dada pelo produto dos catetos dividido por 2.
Sabemos que um dos catetos é o lado menor do retângulo enquanto o outro cateto está oposto ao ângulo de 30o, conseguimos calcular usando as propriedades trigonométricas.
Se um cateto vale 2, calculamos o outro (x) usando
tg(30o) = √3/3
E
tg(30o) = x/2
Então
√3/3 = x/2
x = 2.√3/3
Então a área é
Aj = (2.√3/3 . 2)/2 = 2.√3/3
O enunciado diz que
√3/3 = 0,58
Entao
Aj = 2 . 0,58 = 1,16 m2
A área total é
A = 2.3 = 6 m2
A razão entre Aj e A nos dará a porcentagem
1,16 / 6 = 19,3%
Alternativa E






