A prefeitura de uma cidade planeja construir três postos de saúde. Esses postos devem ser construídos em locais equidistantes entre si e de forma que a distância desses três postos ao hospital dessa cidade sejam iguais. Foram conseguidos três locais para a construção dos postos de saúde que apresentam as características desejadas, e que distam 10 km entre si, conforme o esquema, no qual o ponto H representa o local onde está construído o hospital; os pontos P1, P2 e P3, os postos de saúde; e esses quatro pontos estão em um mesmo plano.
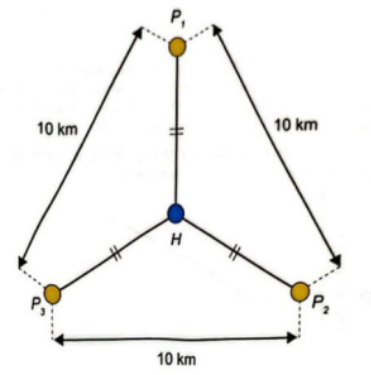
A distância, em quilômetro, entre o hospital e cada um dos postos de saúde, é um valor entre
A) 2 e 3.
B) 4 e 5.
C) 5 e 6.
D) 7 e 8.
E) 8 e 9.
Resolução
Temos na figura um triângulo equilátero de lado 10 km, formado pela junção dos pontos P1, P2 e P3. Pelo fato de ser um triângulo equilátero, sabe-se que os pontos de baricentro, incentro e circuncentro encontram-se no mesmo ponto, no qual, no caso da questão é o ponto H, o qual divide a altura numa razão de 2:1. Sendo então a distância de H até cada um dos postos igual a 2/3 da altura de um triângulo equilátero, encontrada pela fórmula L√3/2.
Sendo assim, como o lado vale 10, temos:
⅔ x 10√3/2
⅔ x 10 x 1,7/2
5,666..
Alternativa C
Veja a resolução com mais detalhes no vídeo abaixo!






