Questão 164 – Progressão aritmética
Em uma corrida de regularidade, cada corredor recebe um mapa com o trajeto a ser seguido e uma tabela indicando intervalos de tempo e distâncias entre postos de averiguação. O objetivo dos competidores é passar por cada um dos postos de averiguação o mais próximo possível do tempo estabelecido na tabela. Suponha que o tempo previsto para percorrer a distância entre dois postos de verificação consecutivos seja sempre de 5 min 15 s, e que um corredor obteve os seguintes tempos nos quatro primeiros postos.
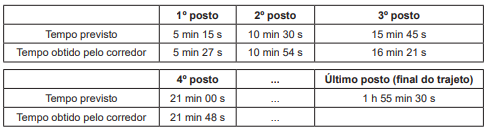
Caso esse corredor consiga manter o mesmo ritmo, seu tempo total de corrida será
A) 1 h 55 min 42 s.
B) 1 h 56 min 30 s.
C) 1 h 59 min 54 s.
D) 2 h 05 min 09 s.
E) 2 h 05 min 21 s.
Resolução
A diferença entre o tempo obtido e o esperado ao primeiro posto foi de
5 min 27 s – 5 min 15 s = 12 s
A diferença entre o tempo obtido e desejado ao segundo posto é
10 min 54 s – 10 min 30 s = 24 s
A diferença entre o tempo obtido e desejado ao terceiro posto é
16 min 21 s – 15 min 45 s = 36 s
A diferença entre o tempo obtido e desejado ao terceiro posto é
21 min 48 s – 21 min = 48 s
podemos observar que a cada etapa, aumenta 12 s na diferença de tempo.
Podemos observar que a diferença de tempo é diretamente proporcional a ordem do posto, no primeiro posto foi
1.12
no segundo
2.12
no terceiro
3.12
no quarto
4. 12
então no n-ésimo será
n.12
o último posto é no tempo 1h 55 min 30s que em segundos é
1.60.60 + 55.60 + 30 = 3600 + 3300 + 30 = 6930 seg
e cada posto demanda 5 min e 15 s inicialmente, ou seja, em segundos
5.60 + 15 = 315 s
Se cada posto é 315 s o último será o
6930/315 = 22o
então o tempo de acréscimo será
22.12 = 264 segundos
adicionando ao tempo previsto
6930 + 264 = 7194 s
vamos ver quanto tempo isso é em hora, min e seg
7194/60 = 119 minutos restando 54 s
119 minutos são
119/60 = 1 hora restando 59 minutos
consequentemente, o tempo total gasto foi
1 h 59 min e 54 s
Alternativa C






