Dois atletas partem de pontos, respectivamente P1 e P2 , em duas pistas planas distintas, conforme a figura, deslocando-se no sentido anti-horário até a linha de chegada, percorrendo, desta forma, a mesma distância (L). Os trechos retos dos finais das curvas até a linha de chegada desse percurso têm o mesmo comprimento (l) nas duas pistas e são tangentes aos trechos curvos, que são semicírculos de centro C. O raio do semicírculo maior é R1 e o raio do semicírculo menor é R2 .
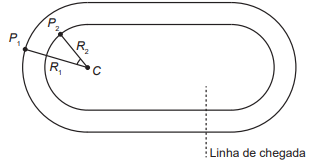
Sabe-se que o comprimento de um arco circular é dado pelo produto do seu raio pelo ângulo, medido em radiano, subentendido pelo arco.
Nas condições apresentadas, a razão da medida do ângulo P2CP1 pela diferença L− l é dada por
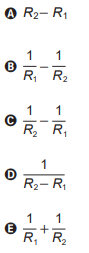
Resolução
Queremos saber a razão entre o ângulo P2CP1 (θ) e a diferença L− l ,
θ / (L – I)
Precisamos calcular a relação entre o comprimento dos arcos e os ângulos.
Sabemos que o arco S1 corresponde ao ângulo α.
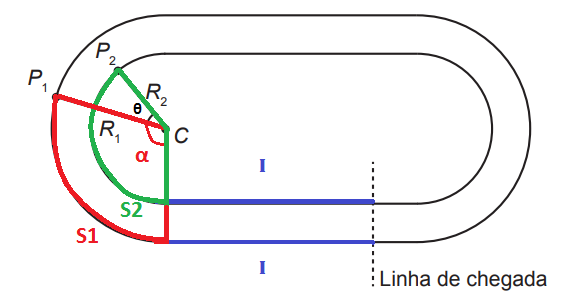
Como os atletas percorrem a mesma distância L, temos que:
L = I + S1 e
L = I + S2,
logo: S1 = S2.
Sendo
S1 = α . R1
S2 = (α + θ) . R2
Podemos então concluir que:
α . R1 = (α + θ) . R2
α . R1 = α . R2 + θ . R2
α . R1 – α . R2 = θ . R2
θ = α . R1 – α . R2
R2
Sendo L – I = S1
Podemos dizer que
L – I = S1
Entao dividindo
θ / S1
teremos
θ/S1 = α . R1 – α . R2 = α . R1/R2 .(α . R1) – α . R2/R2 .(α . R1)
R2 .(α . R1)
Simplificando as frações:
θ/S1 = 1/R2 – 1/R1
Alternativa C






