Questão 165 – Análise Combinatória
Um artesão de jóias tem à sua disposição pedras brasileiras de três cores: vermelhas, azuis e verdes.
Ele pretende produzir joias constituídas por uma liga metálica, a partir de um molde no formato de um losango não quadrado com pedras nos seus vértices, de modo que dois vértices consecutivos tenham sempre pedras de cores diferentes.
A figura ilustra uma joia, produzida por esse artesão, cujos vértices A, B, C e D correspondem às posições ocupadas pelas pedras.
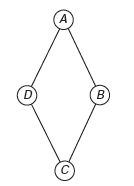
Com base nas informações fornecidas, quantas joias diferentes, nesse formato, o artesão poderá obter?
A) 6
B) 12
C) 18
D) 24
E) 36
Solução
Temos algumas opções:
Cores iguais em vértices opostos: temos 3 escolhas para os vértices A e C, e restam 2 opções para os vértices D e B.
3.2 = 6
Três cores seguidas nos vértices A, B e C, sendo obrigatório repetir em D a cor que se encontra em B: Temos 3 opções para A, 2 para B e D e 1 para C.
3.2.1 = 6,
mas rotacionando a joia podemos notar ela não muda, ou seja está ocorrendo repetição, então devemos dividir esse número por 2.
6/2 = 3
Mesma cor nos vértices A e C e cores diferentes nos vértices B e D: 3 opções para A e C, 2 opções para B e 1 para D, mas ocorre a mesma situação que a anterior então faremos:
3.2.1/2 = 3
Somando todas as combinações temos
6 + 3 + 3 = 12
Alternativa B






