Questão 165 – Geometria Plana
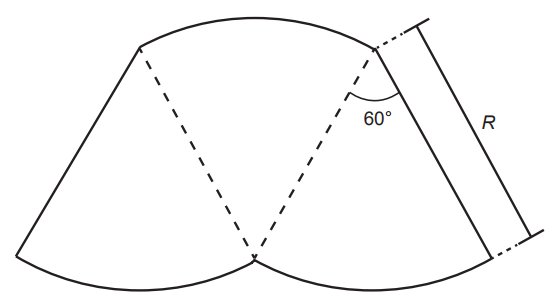
O proprietário de um parque aquático deseja construir uma piscina em suas dependências. A figura representa a vista superior dessa piscina, que é formada por três setores circulares idênticos, com ângulo central igual a 60°. O raio R deve ser um número natural.
O parque aquático já conta com uma piscina em formato retangular com dimensões 50 m x 24 m.
O proprietário quer que a área ocupada pela nova piscina seja menor que a ocupada pela piscina já existente.
Considere 3,0 como aproximação para π.
O maior valor possível para R, em metros, deverá ser
A) 16.
B) 28.
C) 29.
D) 31.
E) 49.
Solução
Cada setor representa uma parte de um círculo de raio r e grau 60, sendo 3 setores de 60 graus, podemos reorganizá-los para que formem um meio círculo (com 180 graus).
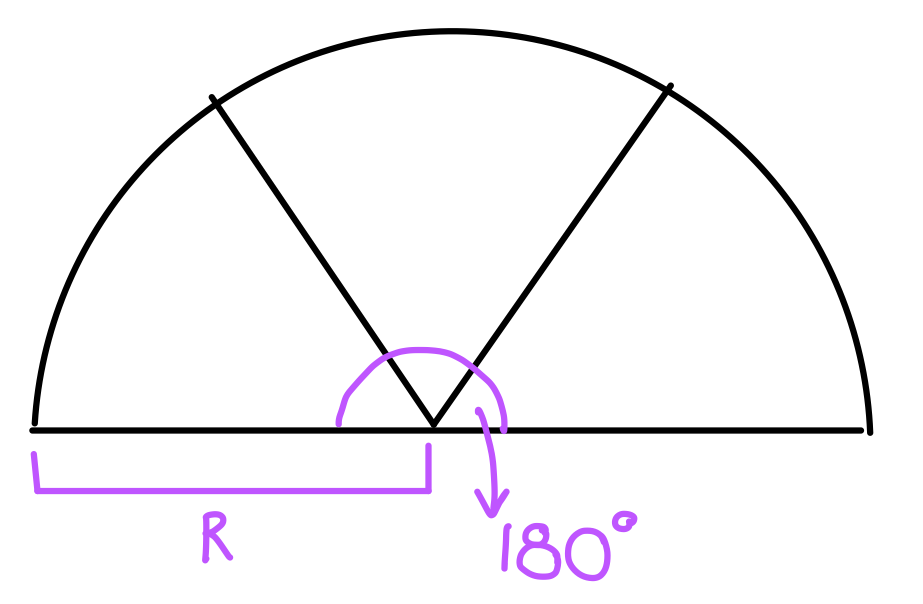
A área então pode ser determinada por
πR2/2
Sendo π = 3
3R2/2
Essa área deve ser menor que a área retangular 50.24 = 1200 m2
3R2/2 < 1200
R2/2 < 1200/3
R2 < 400.2
R2 < 800
R < √800
Fatorando 800
R < 20√2
Das alternativas o número maior mais próximo é 28 (pode se fazer por tentativa a erro elevando cada alternativa ao quadrado e ver qual chega mais próximo de 800)
Alternativa B






