Questão 165 – Análise Combinatória
Uma costureira tem à sua disposição pelo menos duas unidades de cada um dos quatro tipos de retalhos retangulares com as estampas e os tamanhos apresentados.
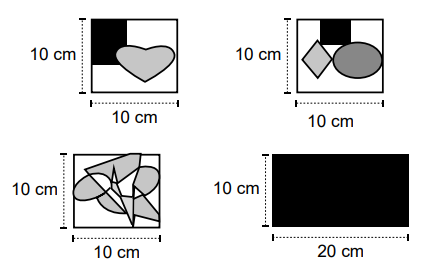
Para confeccionar um tapete em formato retangular de 10 cm x 50 cm, ela utilizará os retalhos, na posição indicada na figura, costurando um lado de um a um lado do outro, sem que haja rotações desses retalhos. O modelo de tapete que pretende confeccionar deverá conter um único retalho de 10 cm x 20 cm e mais três retalhos de formato 10 cm x 10 cm, sendo que retalhos de mesma estampa não poderão ficar lado a lado.
Quantos modelos diferentes de tapetes poderão ser confeccionados?
A) 12
B) 24
C) 34
D) 48
E) 60
Solução
Temos um tapete em formato retangular de 10 x 50 cm e vamos dividí-lo em 5 quadrados de 10 x 10 cm.

Sabemos que vamos usar um retalho de estampa preta de 10 x 20 cm e três retalhos de 10 x 10 cm.
Conseguimos concluir que existem 4 possíveis posições para o retalho preto.
Fixando o retalho preto nos dois primeiros quadrados, podemos observar que o próximo espaço pode ser preenchido com um dos 3 outros retalhos restantes.
Como o próximo espaço não pode ser o mesmo retalho repedido, so nos restas os outros dois, o mesmo serve para o ultimo espaço.

O mesmo acontece com o seu simétrico, como ilustrado abaixo

Então temos
2.(3.2.2) = 24 possibilidades
Fixando o retalho preto no segundo e terceiro quadrado, podemos posicionar 3 opcoes de retalhos no primeiro quadrado, 3 opções no quarto e 2 opções no último já que uma delas não pode repetir ao lado da outra.

O mesmo acontece com o seu simétrico
Temos então
2.(3.3.2) = 36 opções
Somando todas as opções temos
24 + 36 = 60 opções
Alternativa E






