A densidade demográfica de uma região é definida como sendo a razão entre o número de habilidades dessa região e sua área, expressa na unidade habitantes por quilômetro quadrado.
Uma região R é subdividida em várias outras, sendo uma delas a região Q. A área de Q é igual a três quartos da área de R, e o número de habitantes de Q é igual à metade do número de habitantes de de R. As densidades demográficas correspondem a essas regiões são denotadas por d(Q) e d(R) .
A expressão que relaciona d(Q) e d(R) é
A) d(Q) = ¼ d(R)
B) d(Q) = ½ d(R)
C) d(Q) = ¾ d(R)
D) d(Q) = 3/2 d(R)
E) d(Q) = ⅔ d(R)
Resolução
É dito no enunciado que a densidade é obtida por meio da razão entre o número de habitantes H e a área A de determinada região. Com isso, sabemos que a densidade de R e Q serão:
d(R) = H/A
Sabemos que
H(Q) = H/2
E
A(Q) = 3A/4
Entao a densidade será
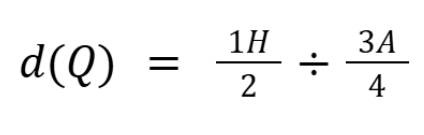
Quando dividimos 2 frações, mantemos a primeira e multiplicamos pelo inverso da segunda, ou seja
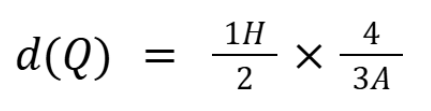
Concluindo que
d(Q) = 2H/3A
d(Q) = 2/3 de H/A
Como sabemos que H/A é igual a dR, temos que dQ equivale a ⅔ de dR.
Alternativa E
Veja a resolução com mais detalhes no vídeo abaixo!






