Um casal e seus dois filhos saíram, com um corretor de imóveis, com a intenção de comprar um lote onde futuramente construiriam sua residência. No projeto da casa, que esta família tem em mente, irão necessitar de uma área de pelo menos 400 m² . Após algumas avaliações, ficaram de decidir entre os lotes 1 e 2 da figura, em forma de paralelogramos, cujos preços são R$ 100 000,00 e R$ 150 000,00, respectivamente.
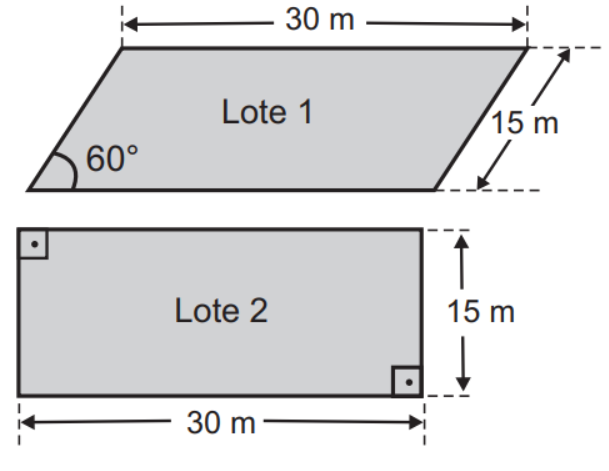
Use √3/2 , 1/2 e 1,7 como aproximações, respectivamente, para sen(60°), cos(60°) e √3 .
Para colaborarem na decisão, os envolvidos fizeram as seguintes argumentações:
Pai: Devemos comprar o Lote 1, pois como uma de suas diagonais é maior do que as diagonais do Lote 2, o Lote 1 também terá maior área;
Mãe: Se desconsiderarmos os preços, poderemos comprar qualquer lote para executar nosso projeto, pois tendo ambos o mesmo perímetro, terão também a mesma área;
Filho 1: Devemos comprar o Lote 2, pois é o único que tem área suficiente para a execução do projeto;
Filho 2: Devemos comprar o Lote 1, pois como os dois lotes possuem lados de mesma medida, terão também a mesma área, porém o Lote 1 é mais barato;
Corretor: Vocês devem comprar o Lote 2, pois é o que tem menor custo por metro quadrado.
A pessoa que argumentou corretamente para a compra do terreno foi o(a)
A) pai.
B) mãe.
C) filho 1.
D) filho 2.
E) corretor.
Solução
Vamos primeiro calcular a área dos lotes
Lote 1: a área é dada por base vezes altura, para encontrar a altura basta reconhecer um triângulo retângulo cuja hipotenusa é 15 m e a altura h é o cateto oposto ao ângulo de 60o
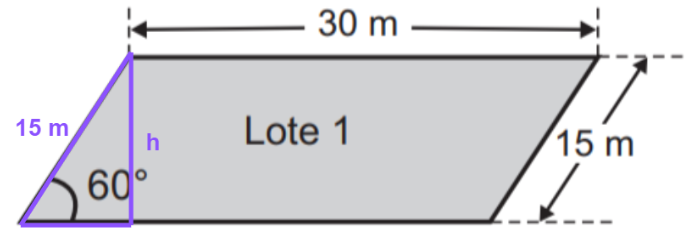
sen60 = √3/2 e sen60 = h/15
Então
√3/2 = h/15
Multiplicando cruzado
2h = 15√3
h = 15√3/2
h = 7,5.1,7 = 12,75 m
A área do lote 1 será
A1 = 30.12,75 = 382,5 m²
A área do lote 2 também é calculada pelo produto de sua altura e base
A2 = 15.30 = 450 m²
Se é preciso de uma área de 400 m² não será possível a aquisição do lote 1 já que sua área é menor, com o Filho 1 disse.
Alternativa C






