Questão 167 – Geometria Espacial
Uma empresa farmacêutica produz medicamentos em pílulas, cada uma na forma de um cilindro com uma semiesfera com o mesmo raio do cilindro em cada uma de suas extremidades. Essas pílulas são moldadas por uma máquina programada para que os cilindros tenham sempre 10 mm de comprimento, adequando o raio de acordo com o volume desejado.
Um medicamento é produzido em pílulas com 5 mm de raio. Para facilitar a deglutição, deseja-se produzir esse medicamento diminuindo o raio para 4 mm, e, por consequência, seu volume. Isso exige a reprogramação da máquina que produz essas pílulas.
Use 3 como valor aproximado para π.
A redução do volume da pílula, em milímetros cúbicos, após a reprogramação da máquina, será igual a
A) 168.
B) 304.
C) 306.
D) 378.
E) 514.
Solução
A seguir apresentamos o formato descrito no enunciado
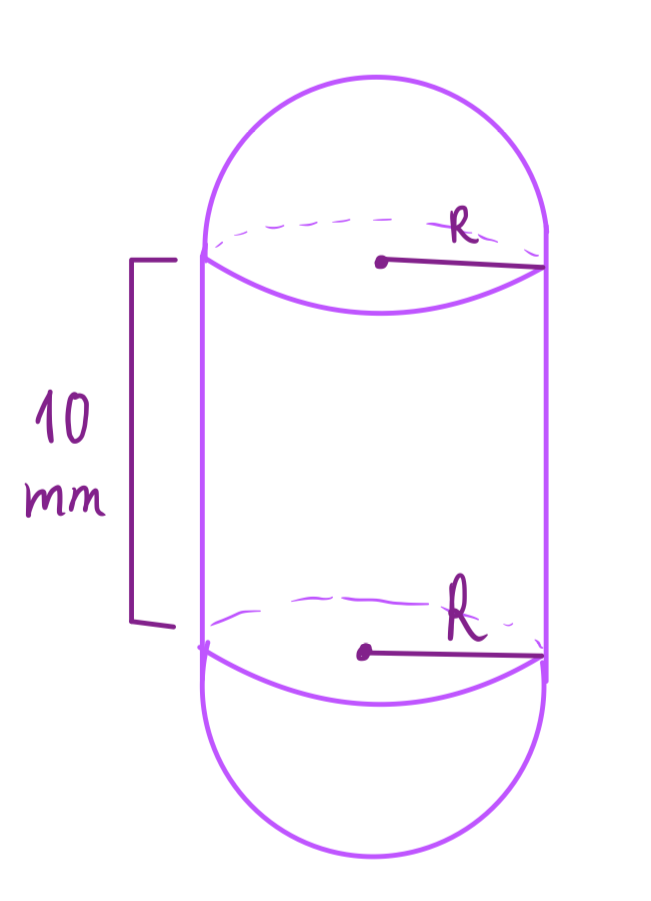
Para calcular o volume com raio 5 mm usaremos a soma do volume de uma esfera de raio 5 e cilindro de raio 5 com altura 10
4πr3/3 + 10πr2 = 4.3.53/3 + 10.3.52
= 500 + 750 = 1250 mm3
Para calcular o volume com raio 4 mm usaremos a soma do volume de uma esfera de raio 4 e cilindo de raio 4 com altura 10
4πr3/3 + 10πr2 = 4.3.43/3 + 10.3.42
= 256 + 480 = 736 mm3
A diferença de um volume para o outro é
1250 – 736 = 514 mm3
Alternativa E






