Questão 168 – Geometria Analítica
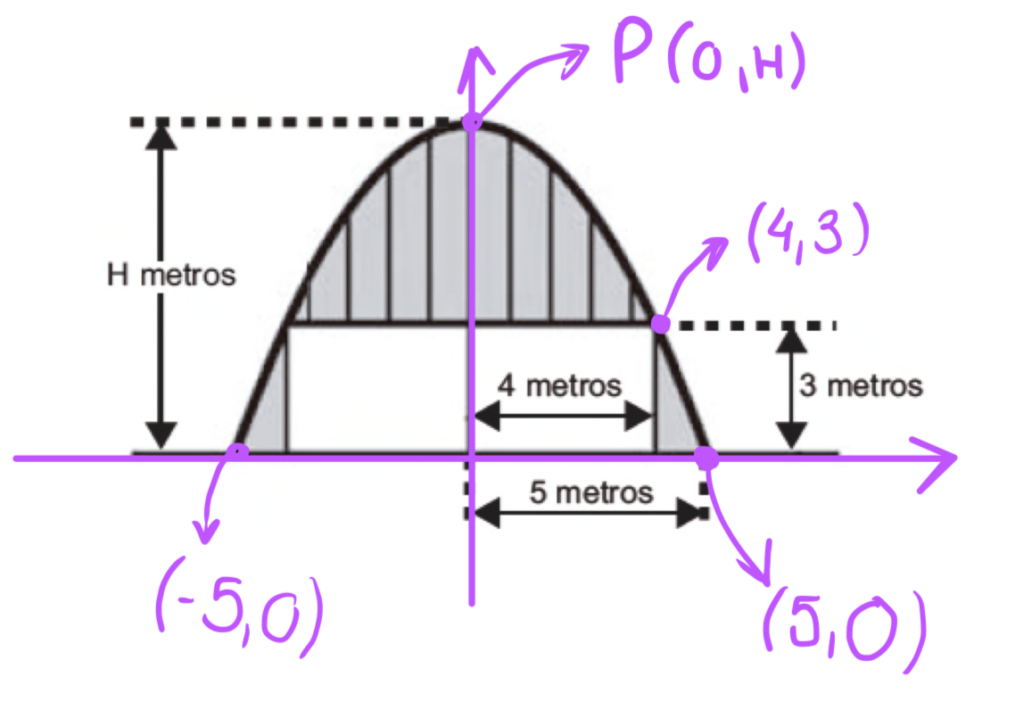
A Igreja de São Francisco de Assis, obra arquitetônica modernista de Oscar Niemeyer, localizada na Lagoa da Pampulha, em Belo Horizonte, possui abóbadas parabólicas. A seta na Figura 1 ilustra uma das abóbadas na entrada principal da capela. A Figura 2 fornece uma vista frontal desta abóbada, com medidas hipotéticas para simplificar os cálculos.
Qual a medida da altura H, em metro, indicada na Figura 2?
A) 16/3
B) 31/5
C) 25/4
D) 25/3
E) 75/2
Solução
É importante pensar na parábola no plano cartesiano com origem no centro da base da abóbada, com isso conseguimos determinar os seguintes pontos: (-5,0), (5,0) e (4,3).
Sendo a função no formato y = ax2 + bx + c, sabemos que c = H, e podemos descobrir os valores de a,b e c substituindo os valores das coordenadas
Substituindo (-5,0):
0 = 25a – 5b + H
Substituindo (5,0):
0 = 25a + 5b + H
Substituindo (4,3):
3 = 16a + 4b + H
Resolvendo o sistema com 3 equações temos
0 = 25a – 5b + H
0 = 25a + 5b + H
3 = 16a + 4b + H
25a – 5b + H = 25a + 5b + H
-5b = 5b
b = 0
Ou seja, agora temos um sistema de duas equações e duas incógnitas
25a + H = 0
16a + H = 3
Se H = -25a
16a – 25a = 3
a = -3/9 = -1/3
Então
H = -25.(-1/3)
H = 25/3
Alternativa D
Veja a resolução com mais detalhes no vídeo abaixo!






