Com o objetivo de reformar os tambores cilíndricos de uma escola de samba, um alegorista decidiu colar adereços plásticos na forma de losango, como ilustrado na Figura 1, nas faces laterais dos tambores. Nesta colagem, os vértices opostos P e Q do adereço deverão pertencer às circunferências do topo e da base do tambor cilíndrico, respectivamente, e os vértices opostos R e S deverão coincidir após a colagem do adereço no tambor, conforme ilustra a Figura 2. Considere que o diâmetro do cilindro correspondente ao tambor meça 0,4 metro. Utilize 3,1 como aproximação para π.
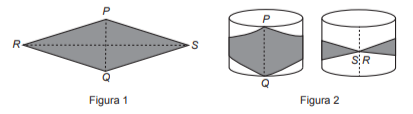
A diagonal RS do adereço a ser confeccionado pelo alegorista deve medir, em metro,
A) 0,124.
B) 0,400.
C) 0,496.
D) 1,240.
E) 2,480.
Solução
Temos que os tambores tem formato cilíndrico. Sabemos que serão colados losangos, dessa forma, o que precisamos é calcular o comprimento da diagonal maior que irá corresponder ao comprimento da circunferência, já que os vértices opostos R e S irão coincidir após a colagem.
Assim temos:
c = 2 . pi. r²
c = 2 . 3,1 . 0,2²
c = 0,4 . 3,1
c = 1,24
Alternativa D






