O cristalino, que é uma lente do olho humano, tem a função de fazer ajuste fino na focalização, ao que se chama acomodação. À perda da capacidade de acomodação com a idade chamamos presbiopia. A acomodação pode ser determinada por meio da convergência do cristalino.
Sabe-se que a convergência de uma lente, para pequena distância focal em metros, tem como unidade de medida a diopria (di).
A presbiopia, representada por meio da relação entre a convergência máxima Cmax (em di) e a idade T (em anos), é mostrada na figura seguinte.
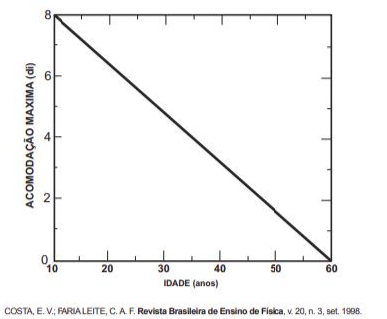
Considerando esse gráfico, as grandezas convergência máxima Cmax e idade T estão relacionadas algebricamente pela expressão
A) Cmax = 2–T
B) Cmax = T2 – 70T + 600
C) Cmax = log2 (T2 –70T + 600)
D) Cmax = 0,16T + 9,6
E) Cmax = –0,16T + 9,6
Solução
No gráfico é dado dois pares ordenados: (60,0) e (10,8) e, por se tratar de uma reta, sabemos que a equação é uma função de primeiro grau. Sendo assim, deve haver: y = ax + b, utilizaremos os dois pares ordenados para encontrarmos o valor de a e b, por meio da montagem de um sistema:
0 = 60a + b
8 = 10a + b . (-1)
0 = 60a + b
-8 = -10a – b (ao somar as duas equações temos:)
-8 = 50a
a = -0,16
Substituindo na segunda equação temos:
8 = 10 . -0,16 + b
8 + 1,6 = b
9,6 = b
Portanto, a função é y = -0,16T + 9,6
Alternativa E






