Questão 168 – ENEM PPL 2016

Na figura estão representadas, em um plano cartesiano, duas circunferências: C₁ (de raio 3 e centro O₁) e C₂ (de raio 1 e centro O₂ ), tangentes entre si, e uma reta t tangente às duas circunferências nos pontos P e Q.

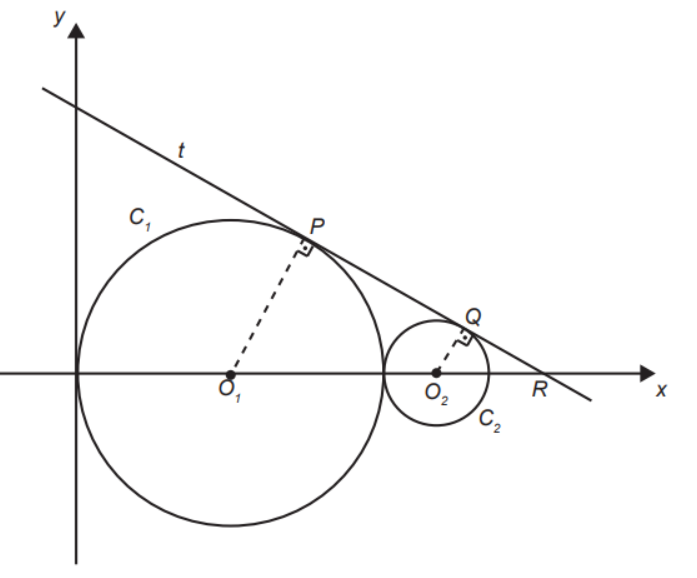
Nessas condições, a equação da reta t é

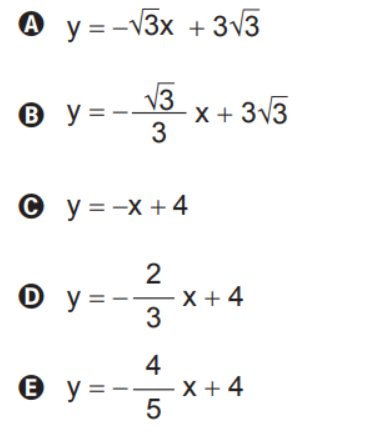
Solução

Precisamos descobrir as coordenadas de pelo menos 2 dos pontos da reta, vamos descobrir R e em seguida descobrir o ângulo que se encontram nesse vértice para por fim descobrir a coordenada do ponto no eixo y.

Podemos observar que os triângulos O₁PR e O₂QR são semelhantes por todos os seus ângulos serem congruentes, isso quer dizer que a razão entre seus lados é igual!

Vamos então comparar as razões

O₁P/O₁R = O₂Q/O₂R

Sendo O₁P o raio da circunferência maior e O₂Q da menor, podemos observar que O₁R é igual a 1 raio da circunferência maior, 2 da menor e um comprimento que chamaremos de A, observado na imagem a seguir.

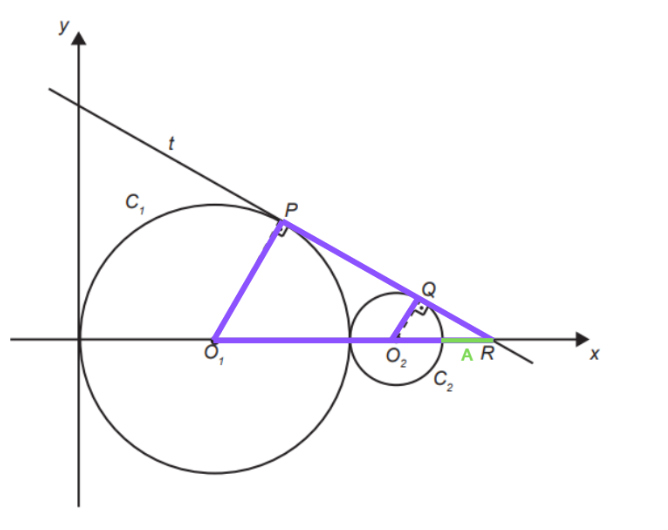
E O₂R é igual a 1 raio da circunferência menor e A.

Então substituindo os valores dos raios e transcrevendo em equação

O₁P/O₁R  = 3/(3+2+A) 

E

O₂Q/O₂R = 1/(1+A)

Igualando

3/(3+2+A) = 1/(1+A)

Multiplicando cruzado e resolvendo temos que

3(1+A) = (3+2+A)

3 + 3A = 5 + A

2A = 2

A = 1 

Com essa informação conseguimos descobrir a coordenada do ponto R já que ele está a distância de 2 raios da circunferência maior, 2 raios da menor e A em relação à origem, ou seja a coordenada de R é

2.3 + 2.1 + 1 = 9

R = (9,0)

Com isso sabemos que o Sen do ângulo em R é o cateto oposto sobre a hipotenusa, usando o triângulo maior para calcular temos

3/(3+2.1+1) = 3/6 = 1/2

Se o sen do ângulo em R é 1/2 sabemos que o único ângulo com esse sen é 30 então R = 30^o

Com essa informação conseguimos calcular o lado do triângulo de vértice na origem T e o ponto em que a reta corta o eixo y S.

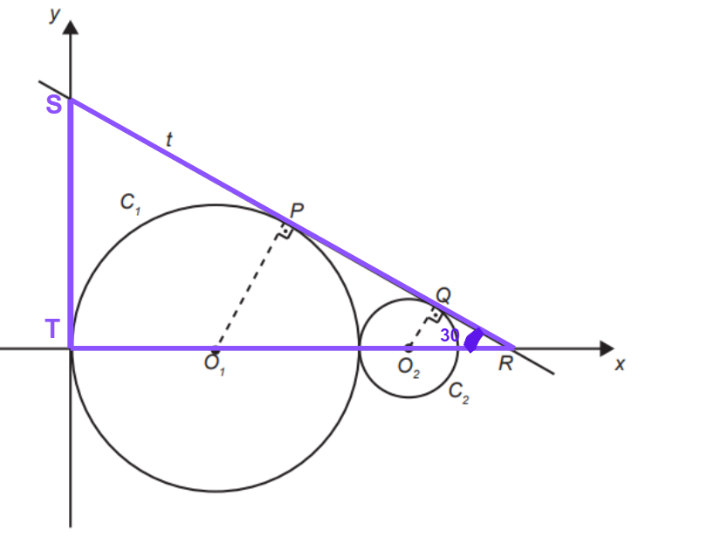
Se Tg 30 = cateto oposto/adjacente, então 

Tg 30 = ST/TR

Sabemos que TR = 2.3 + 2.1 + 1 = 9

Então

Tg 30 = ST/9

Sabemos que Tg 30 =  √3/3, então

ST/9 = √3/3

ST = 9√3/3

ST = 3√3

Se ST é 3√3 então as coordenadas do ponto que passa pelo eixo y é

T = (0; 3√3)

Sabemos que na função de 1o grau y = ax + b, b é o ponto em que corta o eixo y, então a função será

y = ax + 3√3

Conseguimos calcular a substituindo os valores do ponto R (9,0) na equação

0 = 9a + 3√3

9a = – 3√3

a = -3√3/9

a = -√3/3

Então a função y é

y = -√3x/3 + 3√3

Alternativa B