Questão 168 – Geometria espacial
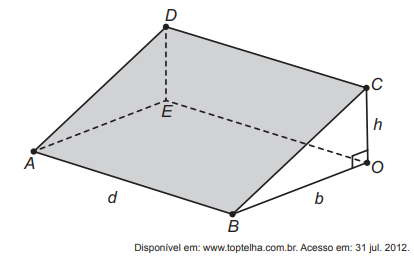
A inclinação de um telhado depende do tipo e da marca das telhas escolhidas. A figura é o esboço do telhado da casa de um específico proprietário. As telhas serão apoiadas sobre a superfície quadrada plana ABCD, sendo BOC um triângulo retângulo em O. Sabe-se que h é a altura do telhado em relação ao forro da casa (a figura plana ABOE), b = 10 é o comprimento do segmento OB, e d é a largura do telhado (segmento AB), todas as medidas dadas em metro.
Sabe-se que, em função do tipo de telha escolhida pelo proprietário, a porcentagem i de inclinação ideal do telhado, descrita por meio da relação
é de 40%, e que a expressão que determina o número N de telhas necessárias na cobertura é dada por N = d2 x 10,5.
Além disso, essas telhas são vendidas somente em milheiros.
O proprietário avalia ser fundamental respeitar a inclinação ideal informada pelo fabricante, por isso argumenta ser necessário adquirir a quantidade mínima de telhas correspondente a
A) um milheiro.
B) dois milheiros.
C) três milheiros.
D) seis milheiros.
E) oito milheiros.
Resolução
Sabemos que d é igual a hipotenusa do triângulo retângulo OBC, para descobrir h que é um dos catetos, precisamos usar a relação descrita pela equação para o valor i = 40% = 0,4, tomando b = 10, temos
0,4 = h.100/10
0,4 = 10h
h = 0,04
Então
d² = b² + h²
substituindo b e h
d² = 10² + 0,04²
d² = 10,0016
Então sendo
N = d² .10,5
N = 100,0016.10,5
N = 1050,0168
Se são mais de mil e menos de 2 mil telhas, precisarei comprar 2 milheiros!
Alternativa B






