Questão 169 – Geometria Plana
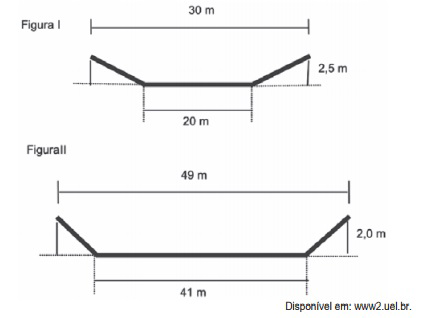
A vazão do rio Tietê, em São Paulo, constitui preocupação constante nos períodos chuvosos. Em alguns trechos, são construídas canaletas para controlar o fluxo de água. Uma dessas canaletas, cujo corte vertical determina a forma de um trapézio isósceles, tem as medidas especificadas na figura I. Neste caso, a vazão da água é de 1.050 m³/s. O cálculo da vazão, Q em m³/s, envolve o produto da área A do setor transversal (por onde passa a água), em m², pela velocidade da água no local, v, em m/s, ou seja, Q = Av.
Planeja-se uma reforma na canaleta, com as dimensões especificadas na figura II, para evitar a ocorrência de enchentes.
Na suposição de que a velocidade da água não se alterará, qual a vazão esperada para depois da reforma na canaleta?
A) 90 m³/s.
B) 750 m³/s.
C) 1.050 m³/s.
D) 1.512 m³/s.
E) 2.009 m³/s.
Solução
Aa área de um trapézio é dada por, sendo b a base menor, B a base maior e h a altura
(B + b).h/2
Aplicando para A1
A1 = (30 + 20).2,5/2
A1 = 62,5 m2
Sabemos que Q1 = 1050 m3/s
Então usando a fórmula dada para calcular v , qué constante, é
1050 = 62,5.v
v = 1050/62,5 = 16,8 m/s
Vamos agora calcular A2 para no fim calcular Q2
A2 = (49 + 41).2/2 = 90 m2
Q2 é dado por
Q2 = 90.16,8
Q2 = 1512 m3/s
Alternativa D






