Questão 169 – ENEM 2013

Questão 169 – Análise Combinatória

Considere o seguinte jogo de apostas:

Numa cartela com 60 números disponíveis, um apostador escolhe de 6 a 10 números. Dentre os números disponíveis, serão sorteados apenas 6. O apostador será premiado caso os 6 números sorteados estejam entre os números escolhidos por ele numa mesma cartela.

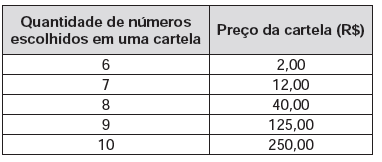
O quadro apresenta o preço de cada cartela, de acordo com a quantidade de números escolhidos.

Cinco apostadores, cada um com R$ 500,00 para apostar, fizeram as seguintes opções:

Arthur: 250 cartelas com 6 números escolhidos;

Bruno: 41 cartelas com 7 números escolhidos e 4 cartelas com 6 números escolhidos;

Caio: 12 cartelas com 8 números escolhidos e 10 cartelas com 6 números escolhidos;

Douglas: 4 cartelas com 9 números escolhidos;

Eduardo: 2 cartelas com 10 números escolhidos.

Os dois apostadores com maiores probabilidades de serem premiados são

A) Caio e Eduardo.

B) Arthur e Eduardo.

C) Bruno e Caio.

D) Arthur e Bruno.

E) Douglas e Eduardo.

Solução

Arthur tem 250 jogos diferentes

Bruno tem

41 . C_7,6 = 41 . 7!/6!1! =41 . 7 = 287 jogos com cartelas de 7

 mais 4 de 6

287 + 4 = 291 jogos diferentes

Caio tem

12. C_8,6 + 10 = 12 . 8!/6!.2!  + 10 = 12.4.7 + 10 = 346 jogos diferentes

Douglas tem 4.C_9,6 = 4 . 9!/6!.3! = 4.3.4.7 = 336 jogos diferentes

Eduardo tem 2.C_10,6 = 2 . 10!/6!.4! = 2.5.3.2.7 = 420 jogos diferentes

Os apostadores com maiores probabilidades de serem premiados são Eduardo e Caio.

Alternativa A