Questão 169 – Escala
A Figura 1 representa uma gravura retangular com 8 m de comprimento e 6 m de altura.
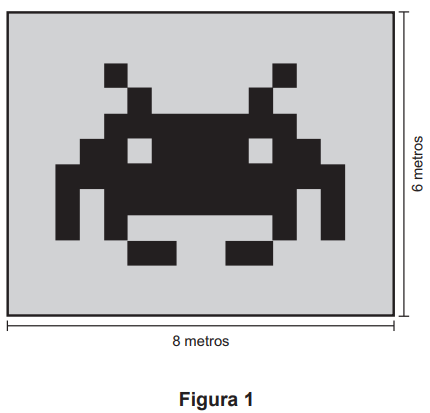
Deseja-se reproduzi-la numa folha de papel retangular com 42 cm de comprimento e 30 cm de altura, deixando livres 3 cm em cada margem, conforme a Figura 2.
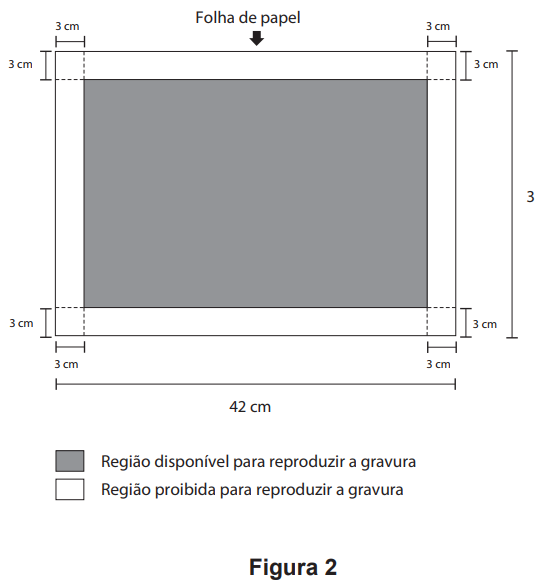
A reprodução da gravura deve ocupar o máximo possível da região disponível, mantendo-se as proporções da Figura 1
PRADO, A. C. Superinteressante, ed. 301, fev. 2012 (adaptado).
A escala da gravura reproduzida na folha de papel é
A) 1 : 3.
B) 1 : 4.
C) 1 : 20.
D) 1 : 25.
E) 1 : 32.
Solução
As dimensões da área útil da folha são 36 e 24 cm
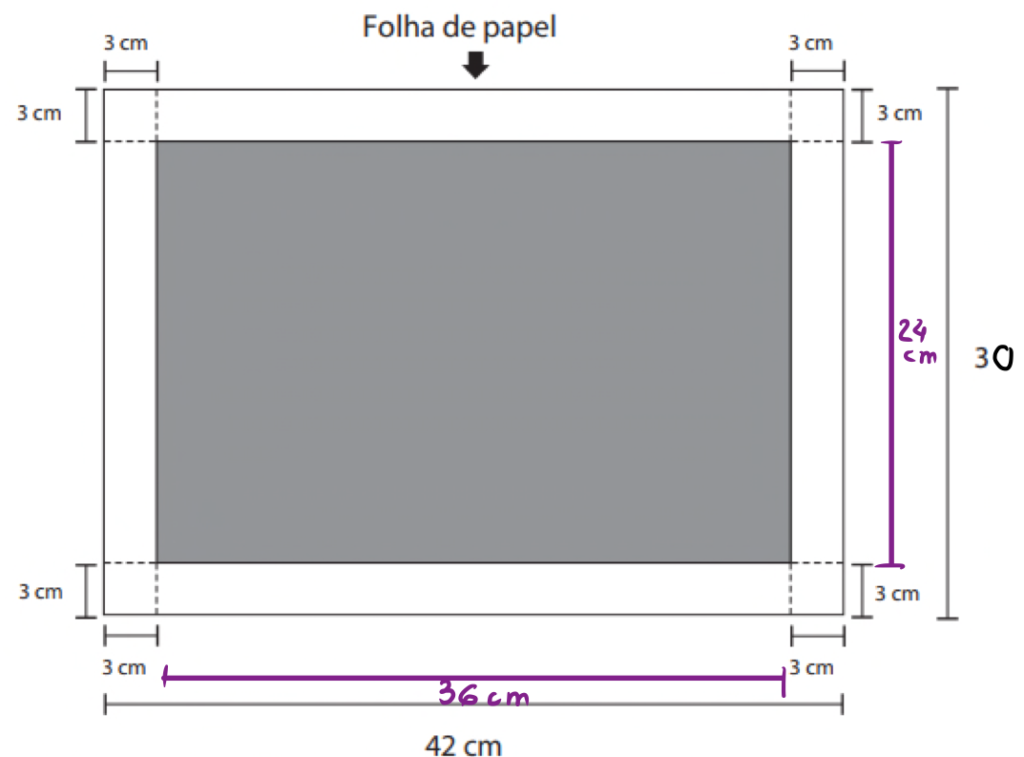
Sendo 1 metro = 100 centímetros
Na horizontal a imagem tem 800 cm enquanto o espaço útil da folha tem 36 cm, então a escala pode ser
36 : 800 = 9 : 200 = 1 : 22,2
Na vertical a imagem tem 600 cm, enquanto o espaço útil da folha tem 24 cm, então a escala pode ser
24 : 600 = 1 : 25
Devemos escolher a menor escala (a que tem o denominador maior), ou seja
1 : 25
Alternativa D






