Questão 170 – Geometria espacial
Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.
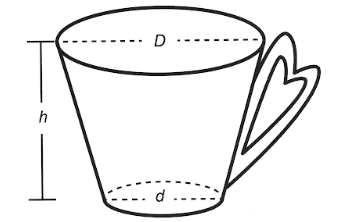
Sabe-se que 1 cm³ = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).
Utilize 3 como aproximação para π.
Qual é a capacidade volumétrica, em milímetro, dessa caneca?
A) 216
B) 408
C) 732
D) 2196
E) 2928
Solução
Para descobrir o volume da xícara, vamos calcular primeiro o volume de um cone de base com diâmetro D cm e subtrair o volume de um cone com diâmetro d cm, como ilustrado abaixo:
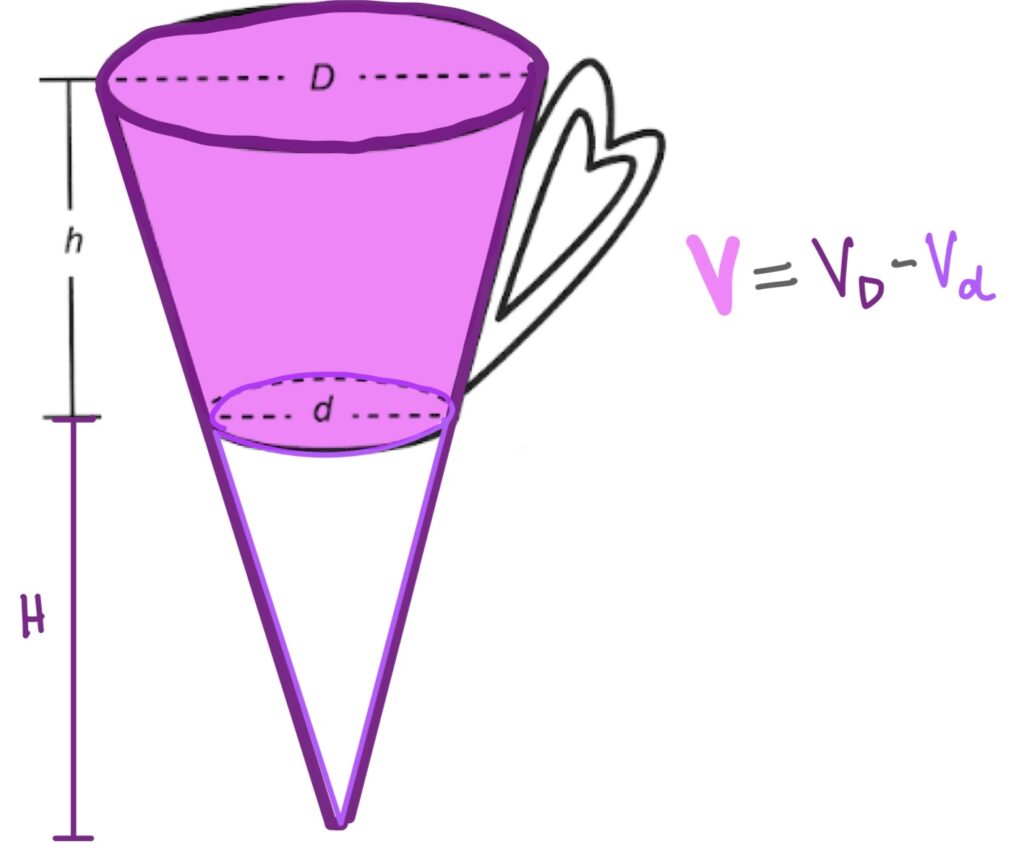
Para calcular H usaremos semelhança de triângulos, sendo h = 12cm
(12 + H)/10 = H/8
96 + 8H = 10H
H = 48
O volume do maior cone é dado por VD= π.R2.(H + h)/3, sendo R = D/2 = 5 cm
VD= π.52.(48 + 12)/3
VD= 1500 cm3
Enquanto Vd= π.r2.H/3
Vd= π.42.48/3
Vd= 1152 cm3
1500 – 768 = 732 cm3
Alternativa C
Veja a resolução com mais detalhes no vídeo abaixo!






