A cobertura de uma tenda de lona tem formato de uma pirâmide de base quadrada e é formada usando quatro triângulos isósceles de base y. A sustentação da cobertura é feita por uma haste de medida x. Para saber quanto de lona deve ser comprado, deve-se calcular a área da superfície da cobertura da tenda.
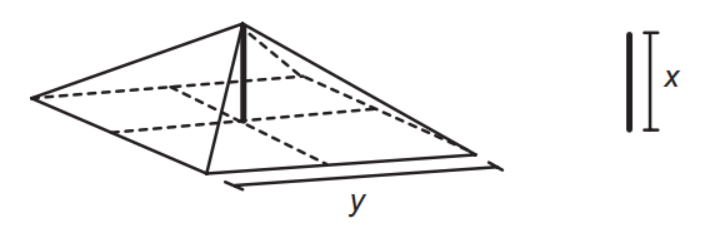
A área da superfície da cobertura da tenda, em função de y e x, é dada pela expressão
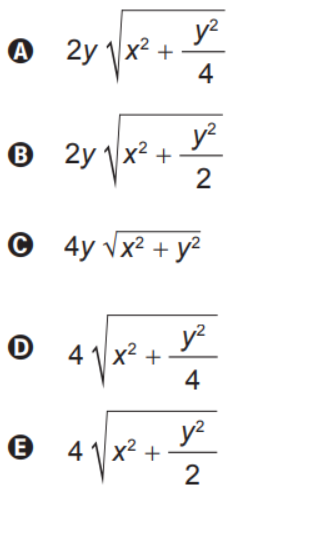
Solução
Podemos observar os seguintes triângulos
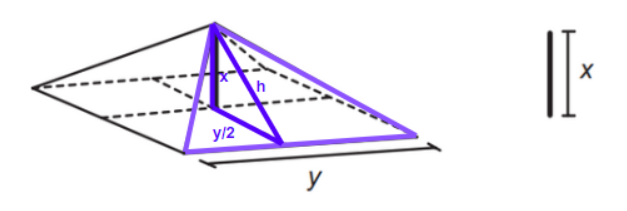
A área superficial será dada por
4.y.h/2 = 2.y.h
o h é calculado usando a fórmula de pitágoras em que h é a hipotenusa
h² = x² + (y/2)²
h = √(x² + y²/4)
Então a área será
2.y.√(x² + y²/4)
Alternativa A






