Questão 171 – ENEM PPL 2011

A torre de Hanói é um jogo que tem o objetivo de mover todos os discos de uma haste para outra, utilizando o menor número possível de movimento, respeitando-se as regras.

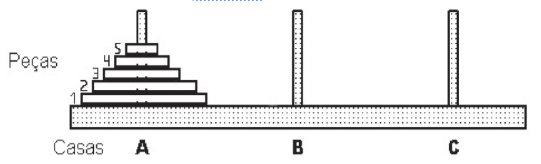
As regras são: 

1- um disco maior não pode ser colocado sobre um disco menor; 

2- pode-se mover um único disco por vez; 

3- um disco deve estar sempre em uma das três hastes ou em movimento.

Disponível em: http://www.realidadevirtual.com.br. Acesso em: 28 abr. 2010 (adaptado). 

Disponível em: http://www.imeusp.br. Acesso em: 28 abr. 2010 (adaptado).

Usando a torre de Hanói e baseando-se nas regras do jogo, podemos montar uma tabela entre o número de peças (X) e o número mínimo de movimentos (Y):

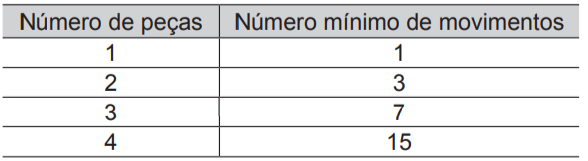
A relação entre (X) e (Y) é 

A) Y = 2^X – 1 

B) Y = 2^{X – 1} 

C) Y = 2^X 

D) Y = 2X – 1 

E) Y = 2X – 4

Solução

Nessa questão é possível resolver substituindo valores nas alternativas. Utilizando as informações da última linha da tabela, temos: X como números de peças = 4 e Y como número mínimo de movimentos =15. 

A) 15 =( 2)⁴  – 1

15=  16 -1 

15=15

B) 15 = 2^4-1 

15 = 2³

15=8

C) 15 = 2⁴ 

15 = 16

D) 15=2.4 -1 

15 = 7

E) 15 = 2.4 – 4

15 = 4

Dessa forma, observamos que a única igualdade verdadeira é a A

Alternativa A