Uma maneira muito útil de se criar belas figuras decorativas utilizando a matemática é pelo processo de autossemelhança, uma forma de se criar fractais. Informalmente, dizemos que uma figura é autossemelhante se partes dessa figura são semelhantes à figura vista como um todo. Um exemplo clássico é o Carpete de Sierpinski, criado por um processo recursivo, descrito a seguir:
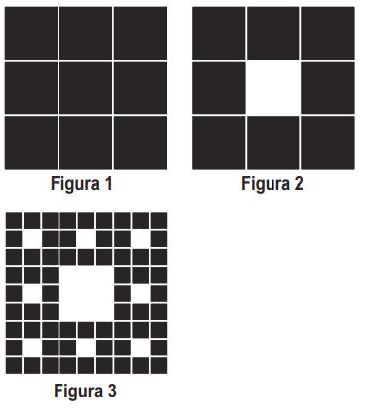
• Passo 1: Considere um quadrado dividido em nove quadrados idênticos (Figura 1). Inicia-se o processo removendo o quadrado central, restando 8 quadrados pretos (Figura 2).
• Passo 2: Repete-se o processo com cada um dos quadrados restantes, ou seja, divide-se cada um deles em 9 quadrados idênticos e remove-se o quadrado central de cada um, restando apenas os quadrados pretos (Figura 3).
• Passo 3: Repete-se o passo 2.
Admita que esse processo seja executado 3 vezes, ou seja, divide-se cada um dos quadrados pretos da Figura 3 em 9 quadrados idênticos e remove-se o quadrado central de cada um deles.
O número de quadrados pretos restantes nesse momento é
A) 64.
B) 512.
C) 568.
D) 576.
E) 648.
Solução
No processo descrito:
Passo 1: O quadrado inicial é dividido em 9 partes e o centro é removido, sobrando 8 quadrados pretos.
Passo 2: Cada um dos 8 quadrados pretos é dividido novamente em 9 partes, removendo-se os centros.
Restam: 8 × 8 = 64 quadrados pretos
Passo 3: Cada um dos 64 quadrados pretos é novamente dividido em 9 partes e os centros são removidos.
Restam: 64 × 8 = 512 quadrados pretos
Alternativa B






