Questão 172 – Geometria Analítica
Devido ao aumento do fluxo de passageiros, uma empresa de transporte coletivo urbano está fazendo estudos para a implantação de um novo ponto de parada em uma determinada rota. A figura mostra o percurso, indicado pelas setas, realizado por um ônibus nessa rota e a localização de dois de seus atuais pontos de parada, representados por P e Q.
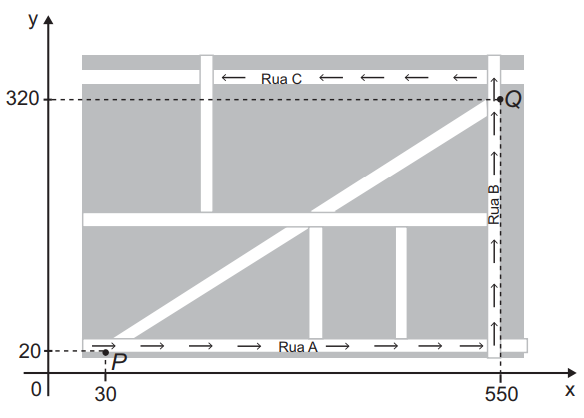
Os estudos indicam que o novo ponto T deverá ser instalado, nesse percurso, entre as paradas já existentes P e Q, de modo que as distâncias percorridas pelo ônibus entre os pontos P e T e entre os pontos T e Q sejam iguais.
De acordo com os dados, as coordenadas do novo ponto de parada são
A) (290 ; 20).
B) (410 ; 0).
C) (410 ; 20).
D) (440 ; 0).
E) (440 ; 20).
Solução
Para calcular a distância entre os pontos P e Q ao longo do percurso basta observar que houveram dois deslocamentos, um na horizontal e outro na vertical.
O deslocamento na horizontal foi da posição 30 à 550 (observando o eixo x), ou seja uma distância de 550 – 30 = 520
O deslocamento na vertical foi da posição 30 à 550 (observando o eixo y), ou seja uma distância de 320 – 20 = 300
Somando essas duas temos a distância total do percurso, e ao dividir ao meio encontramos o ponto equidistande de P e Q
520 + 300 = 820
820/2 = 410
Começando de P e andando 410 horizontalmente nos encontramos na coordenada 410 + 30 = 440 do eixo x, e continuamos na coordenada y do ponto P, y = 20
Par ordenado (440,20)
Alternativa E






