Questão 172 – Geometria Espacial
No período de fim de ano, o síndico de um condomínio resolveu colocar, em um poste, uma iluminação natalina em formato de cone, lembrando uma árvore de Natal, conforme as figuras 1 e 2.
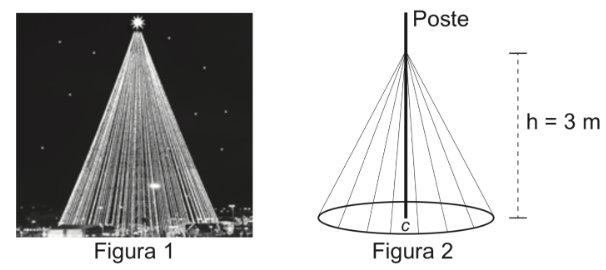
A árvore deverá ser feita colocando-se mangueiras de iluminação, consideradas segmentos de reta de mesmo comprimento, a partir de um ponto situado a 3 m de altura no poste até um ponto de uma circunferência de fixação, no chão, de tal forma que esta fique dividida em 20 arcos iguais. O poste está fixado no ponto C (centro da circunferência) perpendicularmente ao plano do chão.
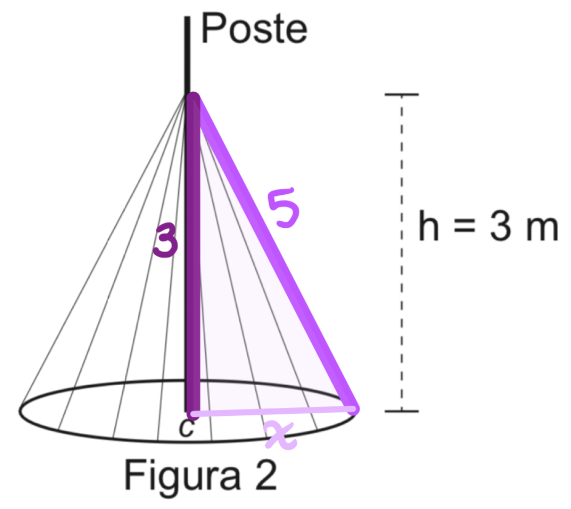
Para economizar, ele utilizará mangueiras de iluminação aproveitadas de anos anteriores, que juntas totalizaram pouco mais de 100 m de comprimento, dos quais ele decide usar exatamente 100 m e deixar o restante como reserva.
Para que ele atinja seu objetivo, o raio, em metro, da circunferência deverá ser de
A) 4,00.
B) 4,87.
C) 5,00.
D) 5,83.
E) 6,26.
Solução
O comprimido total dos 20 arcos é 100 m, então cada arco tem 5 m de comprimento, com a altura e a base é formado um triângulo retângulo:
Por Pitágoras temos
52 = 32 + x2
x2 = 16
x = 4
Alternativa A
Veja a resolução com mais detalhes no vídeo abaixo!






