Em uma das paredes de um depósito existem compartimentos de mesmo tamanho para armazenamento de caixas de dimensões frontais a e b. A terceira dimensão da caixa coincide com a profundidade de cada um dos compartimentos. Inicialmente as caixas são arrumadas, em cada um deles, como representado na Figura 1.
A fim de aproveitar melhor o espaço, uma nova proposta de disposição das caixas foi idealizada e está indicada na Figura 2. Essa nova proposta possibilitaria o aumento do número de caixas armazenadas de 10 para 12 e a eliminação de folgas.
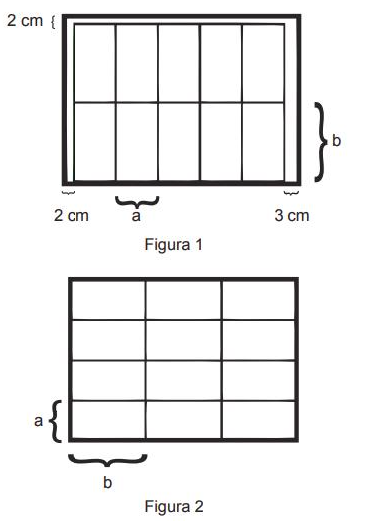
É possível ocorrer a troca de arrumação segundo a nova proposta?
A) Não, porque a segunda proposta deixa uma folga de 4 cm na altura do compartimento, que é de 12 cm, o que permitiria colocar um número maior de caixas.
B) Não, porque, para aceitar a segunda proposta, seria necessário praticamente dobrar a altura e reduzir à metade a largura do compartimento.
C) Sim, porque a nova disposição das caixas ficaria acomodada perfeitamente no compartimento de 20 cm de altura por 27 cm de largura.
D) Sim, pois efetivamente aumentaria o número de caixas e reduziria o número de folgas para apenas uma de 2 cm na largura do compartimento.
E) Sim, porque a nova disposição de caixas ficaria acomodada perfeitamente no compartimento de 32 cm de altura por 45 cm de largura.
Solução
Precisamos analisar as dimensões comparando as figuras.
A figura 1 horizontalmente tem
2 + 5a + 3 = 5 + 5a
E verticalmente
b + b + 2 = 2b + 2
Na figura 2 horizontalmente tem
b + b + b = 3b
E verticalmente
a + a + a + a = 4a,
Precisamos garantir que as dimensoes da figura 1 sejam iguais as da figura 2.
Horizontalmente: 5 + 5a = 3b -> 5a – 3b = -5
Verticalmente: 2b + 2 = 4a -> 2b – 4a = -2 dividindo por 2-> b – 2a = -1
Podemos então formar um sistema de equações
5a – 3b = -5
b – 2a = -1
Isolando o b na segunda equação temos que
b = 2a – 1
Substituindo na primeira equação
5a – 3(2a -1) = -5
5a – 6a + 3 = -5
-a = -8
a = 8 cm
Substituindo esse valor na equação anterior
b = 2.8 – 1
b = 16 – 1
b = 15 cm
Se foi possível encontrar valores positivos para a e b, então é possível e as dimensões da figura são
3b de largura = 3.15 = 45 cm
4a de altura = 4.8 = 32 cm
Alternativa E






