Enchem-se, segundo vazões constantes e idênticas, dois reservatórios, um em forma de um cilindro circular reto e outro em forma de prisma reto de base quadrada, cujo lado da base tem a mesma medida do diâmetro da base do primeiro reservatório.
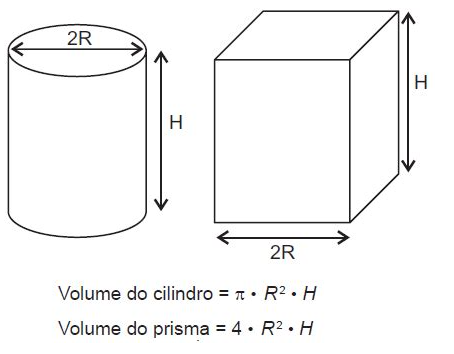
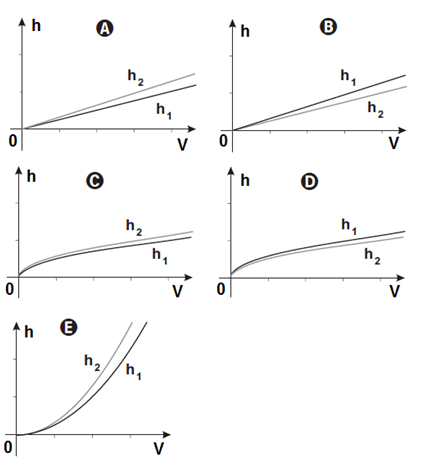
O gráfico que representa a variação das alturas dos níveis da água do reservatório cilíndrico (h₁) e do reservatório em forma de prisma (h₂) em função do volume de água contido em cada um dos reservatórios (V) estão melhor representados em
Solução
É notório que tanto no cilindro quanto no prisma tem uma base regular durante toda a altura, ou seja, não há variação na forma, devido a esse ponto, o gráfico que descreve a variação do volume dos níveis de água do reservatório será uma reta, assim, elimina-se as alternativas C e D. Podemos também eliminar a alternativa E, pois, mostrar um crescimento exponencial, o que não se aplica, devido a uma vazão constante devido ao formato dos sólidos.
Assim, ficamos com as alternativas A e B. Supondo 3 para o valor de pi e 1 para a altura, ao calcular o volume temos que o prisma demanda um volume maior, o que faz a altura irá subir um pouco mais devagar comparado com o cilindro, assim, temos que o gráfico B é o que atende o proposto pela questão.
Alternativa B






